1. Illustration géométrique de l'identité (a+b)²

L'aire totale de la figure ci-contre est celle d'un carré de côté a+b soit (a+b)2. On peut décomposer cette figure en deux carrés de côtés respectifs a et b et deux rectangles de côtés a et b. L'aire totale est donc la somme de l'aire du carré rouge, de l'aire du carré bleu et de l'aire des deux rectangles jaunes. On a : (a+b)2 = b2 +a2 + 2×a×b Soit encore : (a+b)2 = a2 + 2ab + b2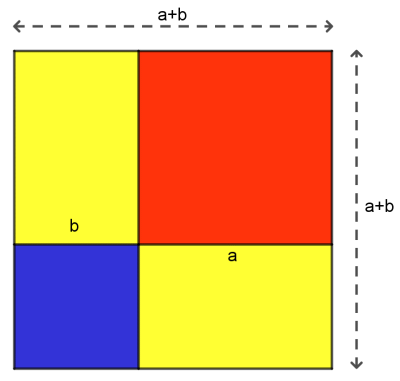

2. Illustration géométrique de l'identité (a-b)²

L'aire en jaune est celle d'un carré de côté a-b. Cette aire peut être obtenue à partir de celle de la figure totale a2, en enlevant les deux rectangles rouge et bleu ont pour côtés a et b. Or ces rectangles se superposent donnant la partie violette hachurée dont l'aire est celle d'un carré de côté b. L'aire du carré jaune est donc la différence entre l'aire totale et l'aire des deux rectangles augmentée de l'aire du carré violet. On a : (a-b)2 = a2 - 2×a×b + b2 Soit encore : (a-b)2 = a2 - 2ab + b2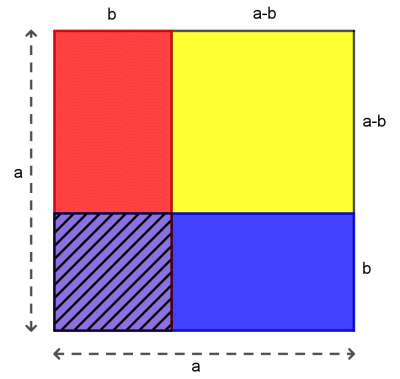

3. Illustration géométrique de l'identité (a+b)(a-b)

L'aire de la partie jaune et de la partie hachuée en bleu foncé est celle d'un rectangle de côtés a-b et a+b. Les deux parties hachurées ont même aire. L'aire de la partie jaune et de la partie hachuée en bleu clair est donc égale à celle du rectangle de côtés a-b et a+b. Cette aire peut être obtenue à partir de celle du carré de côté a en enlevant l'aire du carré rouge de côté b. On a : (a-b)(a+b) = a2 - b2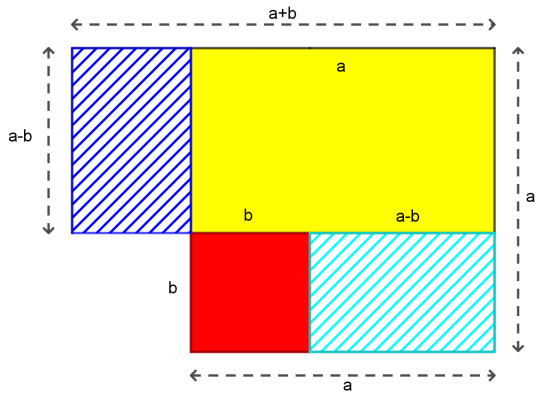