Trouver les valeurs de x et y vérifiant le système :

	{	2x + 3y = 7	(E1)
		8x - y = 2	(E2)

On désigne par (E₁) la première équation et par (E₂) la seconde.

Méthode par combinaisons :

On réalise les combinaisons suivantes :
 (E₁) + 3(E₂) et 4(E₁) -  (E₂)

On obtient un système équivalent :

{	2x + 3y + 24x - 3y = 7 + 6 8x + 12y - 8x + y = 28 - 2	⇔	{	26x = 13 13y = 26
⇔			{	x = 1/2 y = 2

Vérification :
(E₁) : 2×(1/2) + 3×2 =1 + 6 = 7 et (E₂) : 8×(1/2) - 2 = 4 - 2 = 2
Le couple (1/2 ; 2) est solution du système proposé.

Méthode par substitution :

A partir de l'équation (E₂) on exprime y en fonction de x.
(E₂) ⇔ y = 8x - 2

On remplace y par l'expression obtenue dans l'équation (E₁).

(E1) ⇔	2x + 3×(8x - 2) = 2
⇔	2x + 24x - 6 = 7
⇔	26x = 13
⇔	x = 1/2

On remplace x par la valeur trouvée dans l'une des équations (E₁) ou (E₂) pour déterminer y.

Avec (E₂), c'est plus simple : y = 8×(1/2) - 2 = 4 - 2 = 2

On vérifie que (1/2; 2) est bien solution... et on conclut.

Méthode graphique:

On mets les deux équations sous la forme y = ax + b

(E1)

⇔

y = -

2 3

x +

7 3

et (E2)

⇔

y = 8x - 2

On trace les deux droites dans un repère orthonormé approprié.
On lit les coordonnées du point d'intersection qui donne le couple (x ; y) solution du système proposé.

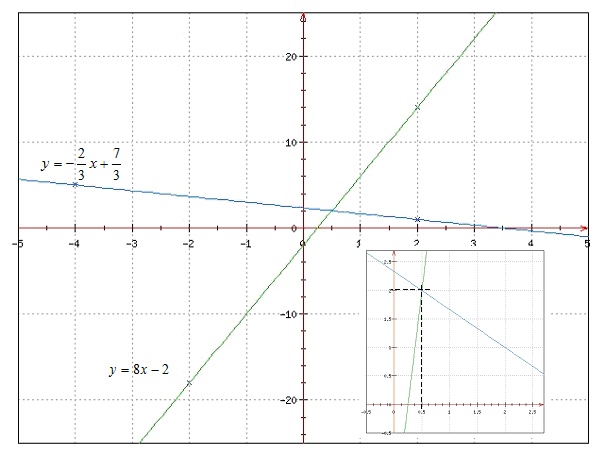
Sans tracer les droites, on peut résoudre l'équation suivant pour trouver x :

-

2 3

x +

7 3

= 8x - 2

⇔

-2x + 7 = 24x - 6

...

On multiplier par 3 pour éviter la manipulation des fractions... On remplace x par la valeur trouvée dans l'une des équations (E₁) ou (E₂). Les deux doivent donner la même valeur de y !