Exemple 2 :Soit ABCD un carré et M un point du segment [BD]. On note P le projeté orthogonal de M sur (AB) et Q le projeté orthogonal de M sur (AD). Démontrer que les droites (PQ) et (CM) sont perpendiculaires. On note a le côté du carré et x la distance PB comme indiqués sur la figure ci-contre. En utilisant par exemple le théorème de Thalès, on peut montrer que PM = PB et QM = QD. De plus, P et Q étant les projetés orthogaunaux de M respectivement sur les droites (AB) et (AD), APMQ est un rectangle. Par conséquent, AQ = PM et AP = QM. En résumé : PM = PB = AQ = x et QM = QD = AP = a - x. Montrons que le produit scalaire→PQ.CM→= 0

→PQ.CM→=	(PA→+→AQ).(CB→+→BP +→PM)
=	→PA.CB→+→PA.BP→+→PA.PM→ +→AQ.CB→+→AQ.BP→+→AQ.PM→
=	0 + (a - x).x + 0 - x.a + 0 + x.x =
=	a.x - x.x - x.a + x.x = 0

Car P ∈ [AB] donc la droite (AP) est perpendiculaires aux droites (BC) et (PM).
→PA.CB→= 0 et→PA.PM→= 0.
Q ∈ [AD], la droite (AQ) est perpendiculaire à la droite (AB) donc à la droite (PB).
→AQ.BP→= 0
Les vecteurs→PA et BP→sont colinéaires et de même sens. De même que les vecteurs→AQ et PM→.
→PA.BP→= PA × BP et→AQ.PM→= AQ × PM.
Les vecteurs →AQ et CB→sont colinéaires et de sens opposé.
→AQ.CB→= - AQ × CB.

Pour conclure, on a bien→PQ.CM→= 0, donc les vecteurs sont orthogonaux et les droites (PQ) et (CM) sont perpendiculaires.

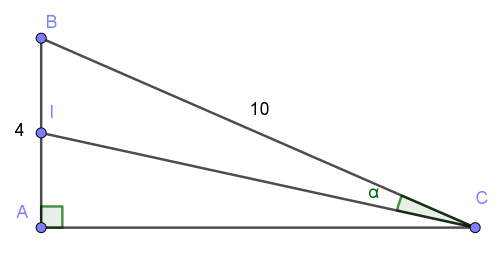
Exemple 3 :On considère un triangle ABC rectangle en A tel que AB = 4 et BC = 10. I est le milieu du segment [AB]. On appelle α l'angle BCI^ 1. Calculer les valeurs exactes de CA et CI. 2. Calculer le produit scalaire →CB.CI→. 3. Donner l'expression de ce produit scalaire en fonction de l'angle α. 4. En déduire la valeur exacte de cos(α), puis celle de sin(α).

1. Le triangle ABC rectangle en A, le théorème de Pythagore s'écrit :
BC² = AB² + AC² d'où AC² = BC² - AB²= 10² - 4² = 100 - 16 = 84 donc AC = √84= 2√21.
Le triangle ACI rectangle en A, le théorème de Pythagore s'écrit :
IC² = AI² + AC² = 2² + 84 = 4 + 84 = 88, donc IC = √88= = 2√22.

2.→CB.CI→=	(CA→+→AB).(CA→+→AI)
=	→CA.CA→+→CA.AI→+→AB.CA→+→AB.AI→
=	CA2 + 0 + 0 + AB×AI = 84 + 4 × 2 = 92.

Car la droite (AC) est perpendiculaire aux droites (AB) et (AI).

3.→CB.CI→= CB × CI × cos(α)

4. cos(α) = →CB.CI→/ CB × CI = 92 / 10×2√22 = 23/5√22