|
| Exemple 1 : Soit U la suite définie pour tout n ∈ ℕ par : Un+1 = |
Un + 1
Un |
et U0 = |
1
2 |
1. Calculer les valeurs de Un jusqu'à n = 15 puis tracer le graphe Un en fonction de n.
Que constate-t-on ?
Les résultats issus d'un code avec AlgoBox sont les suivants :
***Algorithme lancé***
Entrer n : 15
U0 = 0.5
U1 = 3
U2 = 1.3333333
U3 = 1.75
U4 = 1.5714286
U5 = 1.6363636
U6 = 1.6111111
U7 = 1.6206897
U8 = 1.6170213
U9 = 1.6184211
U10 = 1.6178862
U11 = 1.6180905
U12 = 1.6180124
U13 = 1.6180422
U14 = 1.6180308
U15 = 1.6180352
***Algorithme terminé***
|
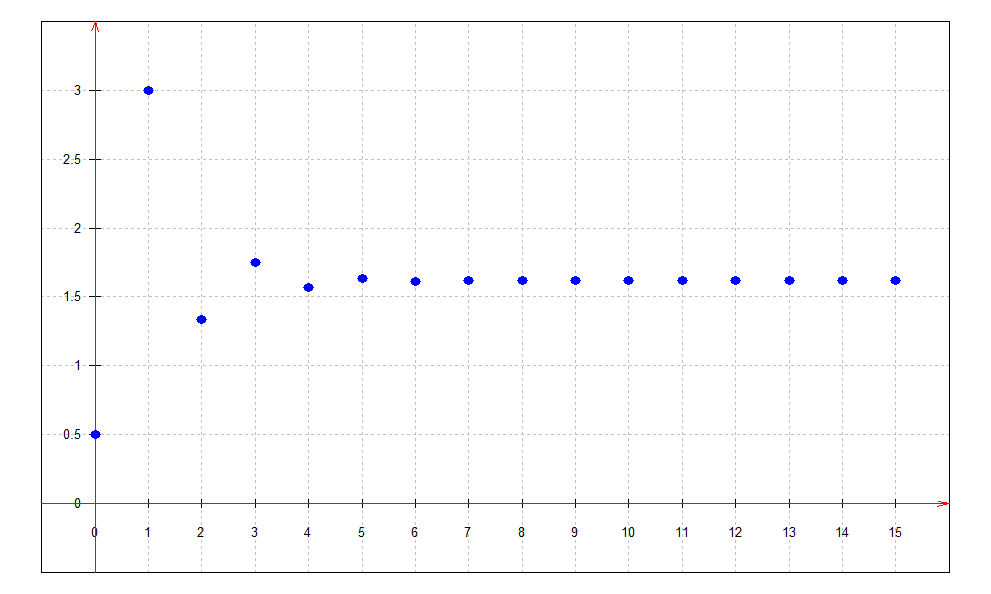 |
On constate que les valeurs se stabilisent autour d'une valeur voisine de 1.61803
|
|
2. Tracer sur un même graphe la droite y = x et la courbe représentative de la fonction
| f(x) = |
x + 1
x |
pour x ∈ ]0 ; +∞[. |
Montrer que les termes de la suite converge vers le point d'intersection de la droite et de la courbe.
En déduire la valeur exacte de la limite de la suite.
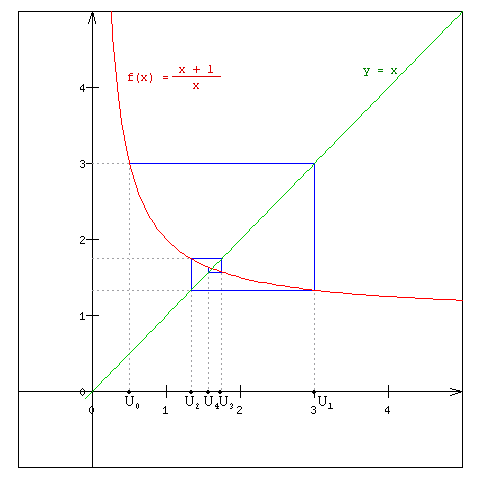 |
On a Un+1 = f(Un).
Graphiquement, en utilisant la courbe de f(x) et la droite y = x pour reporter les valeurs successives de la suite,
on constate que ces valeurs "tournent" autour du point d'intersection de la courbe et de la droite.
Ce point est donc solution de l'équation f(x) = x, soit :
x + 1
x |
= x |
⇔ |
x + 1 = x×x (car x ≠ 0). |
| ⇔ |
x2 - x - 1 = 0. |
Le discriminant de cette équation est
Δ = b2 - 4ac avec a = 1; b = -1; c = -1.
Δ = (-1)2 - 4×1×(-1) = 1 + 4 = 5.
Δ > 0 ; l'équation admet deux racines distinctes:
| x1 = |
-b - √Δ
2a |
= |
1 - √5
2 |
ne convient pas
car < 0 |
| x2 = |
-b + √Δ
2a |
= |
1 + √5
2 |
valeur exacte
de la limite de U |
|
|