Orientation
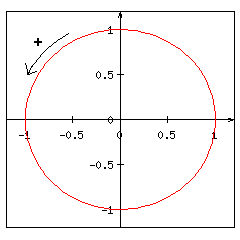
Un cercle peut être parcouru en tournant dans un sens ou dans l'autre. Par convention, le sens positif ou direct est le sens contraire des aiguilles d'une montre.
On parle alors de plan orienté.
La mesure d'un angle entre deux vecteurs→u et→v non nuls est notée (u→,→v).
Elle est comptée positivement lorsqu'on passe du vecteur→u au vecteur→v en tournant dans le sens direct et négativement
lorsqu'on passe du vecteur→u au vecteur→v en tournant dans le sens inverse.
|
 |
Si on fait un ou plusieurs tours complets du cercle trigonométrique dans un sens ou dans l'autre on revient au point de départ.
Il en résulte que la mesure d'un angle est définie à 2kΠ près avec k ∈ ℤ ou modulo 2Π.
| On notera par exemple : (u→,→v) = |
Π
6 |
+ 2kΠ, k ∈ ℤ ou (u→,→v) = |
Π
6 |
(modulo 2Π) |
Mesure principale
Parmi toutes les mesures possibles d'un angle, il en existe une dans l'intervalle ]-Π ; Π],
c'est la mesure principale.
Plusieurs méthodes permettent de trouver cette valeur.
Méthode 1
Pour trouver la mesure principale d'un angle donné α.
| On recherche l'entier relatif k tel que : | -Π < α + 2kΠ ≤ Π |
| En retranchant α a chaque membre on obtient : | -Π - α < 2kΠ ≤ Π - α |
| En divisant par 2Π, l'encadrement de k s'écrit : |
|
|
|
| Si l'angle peut s'écrire α = a Π, alors k vérifie : |
-1 - a
2 |
< k ≤ |
1 - a
2 |
| k est donc le premier entier relatif inférieur à |
1 - a
2 |
ou |
1
2 |
(1 - a). |
| Exemple 1 : Trouver la mesure principale des angles |
19Π
3 |
et |
-55Π
4 |
1
2 |
(1 - |
19
3 |
) = |
-16
6 |
= |
-8
3 |
≃ -2,66 donc k = -3 |
19
3 |
Π - 3×2Π |
= |
19 - 3×6
3 |
Π = |
1
3 |
Π = |
Π
3 |
La mesure principale de |
19Π
3 |
est |
Π
3 |
1
2 |
(1 + |
55
4 |
) = |
59
8 |
= 7,375 donc k = 7 |
-55
4 |
Π + 7×2Π |
= |
-55 + 4×14
4 |
Π = |
1
4 |
Π = |
Π
4 |
La mesure principale de |
-55Π
4 |
est |
Π
4 |
Méthode 2
Pour trouver la mesure principale d'un angle donné α tel que :
| α = |
p
q |
Π, p et q étant des entiers relatifs. |
On recherche le nombre de fois que l'on trouve 2q dans p de sorte que :
p = k × 2q + r où k et r sont des entiers relatifs avec -q < r ≤ q.
| Exemple 2 : Donner la mesure principale des angles |
2014Π
7 |
et |
-31Π
5 |
| 2014 = 144×2×7 -2 donc |
2014Π
7 |
= |
(144×2×7 - 2)Π
7 |
= |
144×2Π - |
2Π
7 |
; |
La mesure
principale de |
2014Π
7 |
est |
-2Π
7 |
|
| -31 = -3×2×5 -1 donc |
-31Π
5 |
= |
(-3×2×5 - 1)Π
5 |
= |
-3×2Π - |
1
5 |
Π |
; |
La mesure
principale de |
-31Π
5 |
est |
-Π
5 |
|
|
