Equations du type cos(x) = cos(y).
En observant le cercle trigonométrique, on constate que cos(α) = cos(-α). Etant donné que les mesures des angles sont définies modulo 2π, on aura :
cos(x) = cos(y) ⇔ x = y + 2kπ, k ∈ ℤ; ou x = -y + 2kπ, k ∈ ℤ .
Equations du type sin(x) = sin(y).
On constate que sin(π - α) = sin(α) donc on pourra écrire :
sin(x) = sin(y) ⇔ x = y + 2kπ, k ∈ ℤ; ou x = π - y + 2kπ, k ∈ ℤ .
Equations du type cos(x) = sin(y) ou sin(x) = cos(y).
On se ramene aux cas précédents en utilsant une formule trigonométrique "tranformant" un sinus en cosinus ou un cosinus en sinus ; sin(α) = cos(π/2 - α) ou cos(α) = sin(π/2 + α). Ainsi :
cos(x) = sin(y) ⇔ cos(x) = cos(π/2 - y) et sin(x) = cos(y) ⇔ sin(x) = sin(π/2 + y) .
Equations du type cos(x) = a ou sin(x) = a.
Si a > 1 ou a < -1 alors les équatiuons n'ont pas de solution car
-1 ≤ cos(x) ≤ 1 et -1 ≤ sin(x) ≤ 1
Si -1 ≤ a ≤ 1 alors on cherche une valeur α telle que cos(α) = a ou sin(α) = a en utisant le tableau des valeurs remarquables.
Si le nombre a n'est pas dans le tableau, on utilise la calculatrice pour donner une valeur approchée. On se ramene ainsi aux cas précédents :
cos(x) = a ⇔ cos(x) = cos(α) ou sin(x) = a ⇔ sin(x) = sin(α) .
Exercice 1 : Soit la fonction f définie par f(x) = 2x3 + 5x2 + x - 2
1. Montrer que f(x) = (x + 1)(2x - 1)(x + 2) puis résoudre l'équation f(x) = 0.
2. En déduire les solutions de l'équation 2cos3(x) + 5cos2(x) + cos(x) - 2 = 0.
|
|
| Exercice 2 : Soit l'équation cos(2x + |
π
4 |
) = |
1
2 |
1. Résoudre l'équation dans ℝ, puis sur les intervalles [0 ; 2π] et [-π ; π]
| On sait que cos( |
π
3 |
) = |
1
2 |
. L'équation s'écrit alors : |
| cos(2x + |
π
4 |
) = |
cos( |
π
3 |
) ⇔ |
2x + |
π
4 |
= |
π
3 |
+ 2kπ, k ∈ ℤ ou 2x + |
π
4 |
= |
-π
3 |
+ 2kπ, k ∈ ℤ |
| ⇔ |
2x = |
-π
4 |
+ |
π
3 |
+ 2kπ, k ∈ ℤ ou 2x = |
-π
4 |
+ |
-π
3 |
+ 2kπ, k ∈ ℤ |
| ⇔ |
2x = |
π
12 |
+ 2kπ, k ∈ ℤ ou 2x = |
-7π
12 |
+ 2kπ, k ∈ ℤ |
| ⇔ |
x = |
π
24 |
+ kπ, k ∈ ℤ ou 2x = |
-7π
24 |
+ kπ, k ∈ ℤ |
| Sur l'intervalle [0 ; 2π] S = { |
π
24 |
; |
25π
24 |
; |
17π
24 |
; |
41π
24 |
} (k= 0 et 1 avec première solution ;
k = 1 et 2 avec seconde solution) |
| Sur l'intervalle [-π ; π] S = { |
π
24 |
; |
-23π
24 |
; |
-7π
24 |
; |
17π
24 |
} (k= 0 et -1 avec première solution ;
k = 0 et 1 avec seconde solution) |
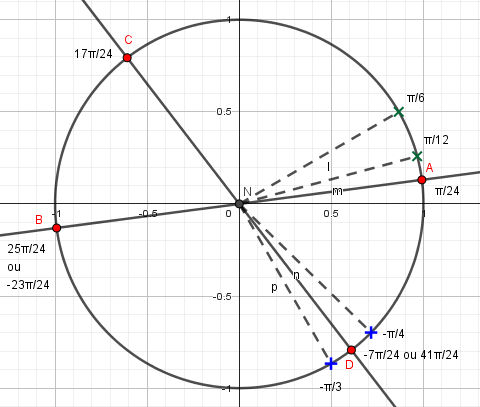
2. Représenter les solutions sur le cercle trigonométrique.
|
Pour placer le point A correspondant à l'angle π/24, on trace la bissectrice de l'angle π/6 donnant un angle de π/12, puis la bissectrice de cet angle.
Le point B est obtenu par symétrie par rapport à l'origine.
Pour placer le point D correspondant à l'angle -7π/24, on trace la bissectrice de l'angle formé par -π/3 et -π/4.
Le point C est obtenu par symétrie par rapport à l'origine.
|
|
|
