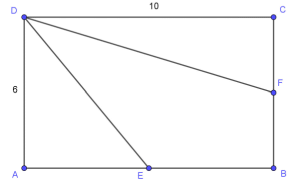
Exemple 1 :On considère le rectangle ABCD de longueur 10 et de largeur 6. E est le milieu du côté [AB] et F le milieu du côté [BC]. Déterminer les valeurs des produits scalaires suivants.
1.→DA.DB→	2.→DC.DF→	3.→DA.DC→
4.→DE.DF→	5.→DF.DB→	6.→AC.CB→

1.Méthode 1 :
→DA.DB→= DA × DB × cos(→DA , DB→) =DA × DB × DA/DB = DA²= 6² = 36
Car le triangle ABD est rectangle en A, donc on a cos(ADB) = DA/DB.

Méthode 2 : →DA.DB→= →DA.DA→ = DA²= 6²= 36
Car le projeté orthogonal de B sur la droite (AD) est A.

Méthode 3 : Utilisation de la relation de Chasles
→DA.DB→=→DA.(DA→+→AB)= →DA.DA→+→DA.AB→ = DA² + 0 = 6² = 36
Car les droites (AD) et (AB) sont perpendiculaires et les vecteurs→DA et AB→orthogonaux.

Méthode 4 :→u.v→=

1 2

(→∥u∥2 +→∥v∥2 - ∥u→-→v∥2) avec →u =→DA et v→= DB→

→u - v→=→DA - DB→=→DA + BD→= BA→

→DA.DB→=	1 2	(DA2 + DB2 - BA2)	Car le triangle ABD est rectangle en A, et d'après Pythagore DB2 = DA2 + AB2.
=	1 2	(DA2 + DA2 + AB2 - BA2)
=	1 2	(2 × DA2) = DA2 = 62 = 36

2. Méthode 2 : →DC.DF→= →DC.DC→ = DC²= 10²= 100
Car le projeté orthogonal de F sur la droite (DC) est C.

3.→DA.DC→= 0. Car les droites (AD) et (CD) sont perpendiculaires (cf. rectangle ABCD) donc les vecteurs →DA et DC→sont orthogonaux.

4.Méthode 3 : Utilisation de la relation de Chasles
→DE.DF→=(DA→+→AE).(DC→+→CF) =→DA.DC→+→DA.CF→+→AE.DC→+→AE.CF→

→DA.DC→= 0. (cf question 3.)

→DA.CF→= DA×CF = 6×3 = 18
Car F milieu de [BC] et dans ce rectangle→DA =→CB = 2×CF→.

→AE.DC→= AE×DC = 5×10 = 50
Car E milieu de [AB] et dans ce rectangle→DC =→AB = 2×AE→.

→AE.CF→= 0. Car les droites (AB) et (BC) sont perpendiculaires et E∈(AB) et F∈(BC) donc les vecteurs→AE et CF→orthogonaux.
Finalement →DE.DF→= 0 + 18 + 50 + 0 = 68.

5.Méthode 3 :Utilisation de la relation de Chasles
→DF.DB→= (DC→+→CF).(DC→+→CB) =→DC.DC→+→DC.CB→+→CF.DC→+→CF.CB→
        = DC² + 0 + 0 + CF×CB = 10²+ 3×6 = 118.

6. Méthode 4' :→u.v→=

1 2

(∥u→+→v∥2 -→∥u∥2 -→∥v∥2) avec →u =→AC et v→= CB→

→u + v→=→AC + CB→=→AB→

→AC.CB→=

1 2

(AB2 - AC2 - CB2) =

1 2

(AB2 - AB2 - BC2 - CB2) =

1 2

(-2×BC2) = -BC2 = -62 = -36

Car le triangle ABC est rectangle en B, donc d'après Pythagore AC² = AB² + BC².

Autre Méthode : On peut calculer tous ces produits scalaires en se plaçant dans un repère orthonormé. Par exemple dans le repère (A;→i,→j) tel que AB→= 10i→et AD→= 6j→. Les coordonnées des points de la figure sont alors : A(0;0) B(10;0) D(0;6) C(10;6) E(5;0) et F(10;3)

1. Les coordonnées des vecteurs sont→DA(0;-6) et→DB(10;-6) →DA.DB→= 0x10 + (-6)x(-6) = 36
2. Les coordonnées des vecteurs sont→DC(10;0) et→DF(10;-3) →DC.DF→= 10x10 + (0)x(-3) = 100
3. Les coordonnées des vecteurs sont→DA(0;-6) et→DC(10;0) →DA.DC→= 0x10 + (-6)x(0) = 0
4. Les coordonnées des vecteurs sont→DE(5;-6) et→DF(10;-3) →DE.DF→= 5x10 + (-6)x(-3) = 50 + 18 = 68
5. Les coordonnées des vecteurs sont→DF(10;-3) et→DB(10;-6) →DF.DB→= 10x10 +(-3)x(-6)= 100+18 = 118
6. Les coordonnées des vecteurs sont→AC(10;6) et→CB(0;-6) →AC.CB→= 10x0 + 6x(-6) = -36