Définitions

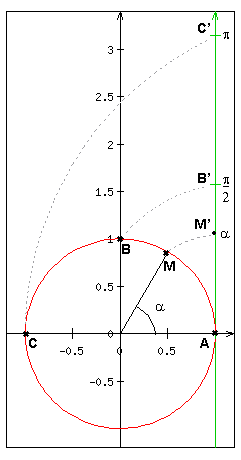
Dans le plan muni d'un repère orthonormé (O,→i,→j), le cercle trigonométrique est le cercle de centre O est de rayon de une unité. On considère le point A du cercle tel que A(1 ; 0) et la tangente au cercle en ce point. Si on "enroule" cette droite autour du cercle, les points B et B', C et C' ou M et M' se superposent. Ainsi, la distance entre le point A et un autre point de la droite est égale à la longueur de l'arc de cercle entre le point A et le point du cercle correspondant au point de la droite après l'enroulement. On a alors : AB' = AB⁀, AC' = AC⁀, AM' = AM⁀ Etant donné que le rayon du cercle est de une unité, son périmètre est de 2Π. L'angle AOC^correspond à 180° et l'arc AC⁀= Π. On peut donc définir une nouvelle échelle le radian (symbole rad ou rd) qui à chaque angle associe la longueur de l'arc du cercle trigonométrique qu'il intercepte. Dans un cercle de rayon r, un angle de 1 rad correspond à la mesure de l'angle au centre qui intercepte un arc d'une longueur égale au rayon. On retiendra la relation :  α (en rad) = α (en °) × Π /180

Introduction aux fonctions trigonométriques

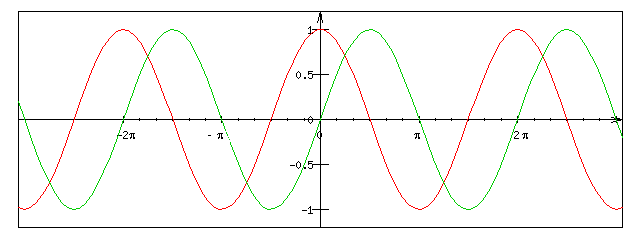
On peut remarquer qu'un point quelconque M du cercle trigonométrique a pour coordonnées :
M(cos α ; sin α). Ainsi, en graduant un axe des abscisses en radian et en reportant sur l'axe des ordonnées les valeurs de l'abscisse et de l'ordonnée du point M, on obtient les courbes représentatives des fonctions cos(x) et sin(x). Ces fonctions sont périodiques de période 2Π.
On a cos(x + 2Π) = cos(x) et sin(x + 2Π) = sin(x).

Valeurs remarquables :

x 0 Π 6 Π 4 Π 3 Π 2 Π cos(x) 1 √3 2 √2 2 1 2 0 -1 sin(x) 0 1 2 √2 2 √3 2 1 0

Si α + β =  Π 2  alors cos(α) = sin(β) et sin(α) = cos(β)