Définitions

Une fonction est une relation qui lie un élément x d'un ensemble de départ à un et un seul élément y d'un ensemble d'arrivée.

Elle est généralement notée f, ainsi on peut écrire y = f(x) que l'on lit "y égal à f de x".

L'élément y est appelé image de x par la fonction f.

L'élément x est appelé antécédent de y par la fonction f.

Pour définir une fonction f, on note :

f : x y = f(x)

L'ensemble des éléments qui admettent une image par la fonction f est appelé ensemble ou domaine de définition de f, on le note D_f.

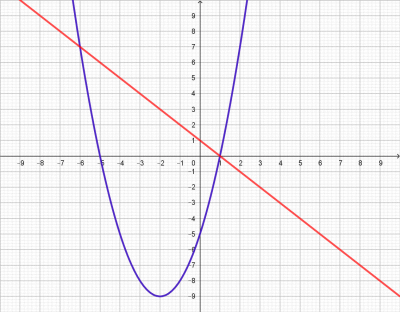
Une fonction peut être définie : * par un programme de calcul :		Fig. 1
	Choisir un nombre; Ajouter 4 à ce nombre; Multiplier le résultat par le nombre de départ; Ajouter -5 au résultat.
* par une "formule" : f(x) = x² + 4x - 5 ou f(x) = -x + 1.
* par sa représentation graphique (Fig.1).
* par un tableau de valeurs.

x	-4	-3	-2	-1	0	1	2	3	4
f(x)	5	2	1	-3	-4	3	5	5	-4

Images
Un nombre a une et une seule image par une fonction.

* Si un programme de calcul est donné, il suffit de choisir un nombre et d'exécuter le programme.
Exemple : Quelles sont les images de -2 et 2 en utilisant le programme page précédente: ?

Nombre Choisi	Ajouter 4	Multiplier par Nombre Choisi	Ajouter -5	L'image de -2 est -9. L'image de 2 est 7.
-2	-2 + 4 = 2	2 × (-2) = -4	-4 + (-5) = -9
2	2 + 4 = 6	6 × 2 = 12	12 + (-5) = 7

* Si l'expression (la formule) de la fonction f est donnée.
On peut calculer l'image d'un nombre en remplaçant x par la valeur donnée.
Si x₀ désigne cette valeur, on calcule f(x₀).
Exemple : Soit la fonction f : x ⟼ 3x² + 4x + 1. Quelle est l'image de -1 ?
Une écriture équivalente à celle donnée est f(x) = 3x² + 4x + 1.
Ici on doit calculer f(-1) = 3×(-1)² + 4×(-1) + 1 = 3 - 4 + 1 = 0.
L'image de -1 par f est 0 ou f(-1) = 0.

* Si on donne un tableau de valeurs, il suffit de trouver un nombre dans la liste des valeurs données (généralement première ligne) et de donner la valeur correspondante.
Exemple : On considére un rectangle de dimensions 4 cm et 𝓁 cm. Le tableau suivant donne les valeurs de son périmètre en fonction de 𝓁. Donner l'image de 2.

Valeurs de 𝓁 en cm	0,5	1	2	3,5	6	L'image de 2 est 12
Valeurs du périmètre en cm	9	10	12	15	20

* Si la fonction est définie par une courbe (sa représentation graphique).

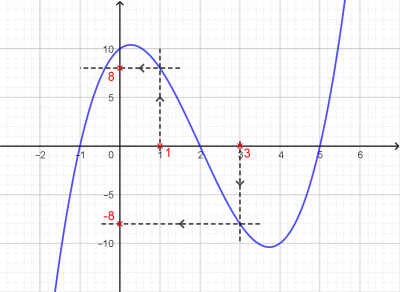Pour trouver l'image d'un nombre donné, on repère celui-ci sur l'axe des abscisses puis on trace la droite parallèle à l'axes des ordonnées passant par ce point jusqu'à atteindre la courbe. A partir de ce point d'intersection, on trace une droite parallèle à l'axe des abscisses. La valeur de l'image se lit alors sur l'axe des ordonnées Soit la fonction f définie par la courbe ci-contre. Quelle est l'image de 1 ? Que vaut f(3) ? L'image de 1 est 8 (on pourrait écrire f(1) = 8). f(3)= -8 (écriture équivalente à la phrase : l'image de 3 par f est -8)