Retour | A Suivre

Antécédents

Un nombre peut avoir un ou plusieurs antécédents par un fonction. Il peut également ne pas avoir d'antécédent !

* Si l'expression (la "formule") de la fonction f est donnée.

On peut trouver le ou les antécédents d'un nombre y0 en résolvant l'équation f(x) = y0.
Si l'équation n'a pas de solution, le nombre choisit n'a pas d'antécédent.
Si l'équation obtenue n'est pas du premier degré, il faut essayer de factoriser pour se ramener à une équation produit nul...

Exemple : Soit la fonction définie par f(x) = x2.
1. Quels sont les antécédents de 4 ?
2. -1 a-t-il des antécédents ?

1. On doit résoudre f(x) = 4, c'est-à-dire x2 = 4 ou x2 - 4 = 0.
En utlilisant une identité remarquable, on peut écrire (x + 2)(x - 2) = 0.
Or un produit de facteurs est nul si l'un des facterus est nul (Règle du produit nul).
On doit donc avoir : x + 2 = 0 ou x - 2 = 0, soit x = - 2 ou x = 2.
Les antécédents de 4 par f sont -2 et 2.

2. On doit résoudre f(x) = -1, c'est-à-dire x2 = -1.
Or un carré est toujours positif, donc l'équation n'a pas de solution.
-1 n'a pas d'antécédent par f.

* Si la fonction est définie par un programme de calcul.

On peut essayer de faire tourner le programme à l'envers.
Si cela n'est pas possible, il faut trouver l'expression obtenue en fin de programme lorsque on choisit un nombre quelconque x. La "formule" est ainsi déterminée. On se ramène alors à la situation décrite précédement.

Programme A   Programme inverse de A    
  • Choisir un nombre;
  • Ajouter 2 à ce nombre;
  • Prendre le carré du résultat obtenu;
  • Soustaire 5 au résultat.
    		•  
  • Avec le nombre donné;
  • Ajouter 5 à ce nombre;
  • Prendre la racine carré du résultat obtenu;
  • Soustaire 2 au résultat.
    		•   Quel nombre doit-on choisir pour que le programme A
    donne -1 ?
    -1 + 5 = 4 ; √4 = 2 ; 2 - 2 = 0.
    Il faut choisir 0 pourque le programme A donne -1 .
    Quel est l'antécédent de 4 par le programme A?
    4 + 5 = 9 ; √9 = 3 ; 3 - 2 = 1.
    1 est l'antécedent de 4 par le programme A.

    Programme B   Programme inverse de B   Le programme inverse de B "bloque" à la 2ème étape !
  • Choisir un nombre;
  • Soustraire 2 à ce nombre;
  • Multiplier le résultat par le nombre de départ;
  • Ajouter 1 au résultat.
    		•  
  • Avec le nombre donné;
  • Soustraire 1 à ce nombre;
  • Diviser par ?;
  • Ajouter 2 au résultat.
    		•   Si on choisit x le programme B conduit à la formule :
    (x - 2)x + 1 = x2 - 2x + 1 = (x - 1)2
    Quels nombres doit-on choisir pour que le programme B donne 9 ? ... On doit résoudre (x - 1)2 = 9
    Sachant que si X2 = a2 alors X = a ou X = -a,
    on en déduit : x - 1 = 3 ou x - 1 = -3
    soit x = 4 ou x = -2.
    Si on choisit 4 ou -2 on obtient 9 avec le programme B.

    * Si la fonction est définie par sa courbe représentative.
    Pour déterminer graphiquement le ou les antécédents d'un nombre y0 par une fonction, on fait le chemin inverse à celui pour déterminer une image.
    On repère la valeur donnée sur l'axe des ordonnées, on trace une parallèle à l'axes des abscisses passant par cette valeur (droite d'équation y = y0). A partir du point ou des points d'intersection avec la courbe représentative de la fonction, on trace des parallèles à l'axe des ordonnées. On lit la ou les valeurs sur l'axe des abscisses.
    Si la droite tracée ne coupe pas la courbe, cela signifie que le nombre donné n'a pas d'antécédent.

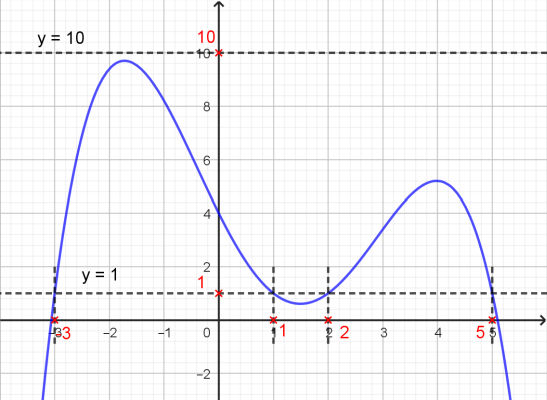
    On considère le fonction f définie par la courbe représentation ci-contre.
    a) Combien d'antécédent possède 1 ? Donner leur valeurs.
    La droite y = 1 coupe la courbe en 4 points. Il y a donc 4 antécédents. Les abscisses de ces points sont -3, 1, 2 et 5.
    Les antécédents de 1 par f sont -3, 1, 2 et 5.

    b) 10 a-t-il des antécédents par cette fonction ?
    La droite y = 10 ne coupe pas la courbe. Il n'existe aucune valeur de x telle que f(x) = 10.
    10 n'a pas d'antécédent.

    * Si la fonction est définie par un tableau de valeurs.