Index | Suite

Combinatoire et dénombrement

On considère deux ensembles E et F qui sont constitués respectivement de n et m éléments.
(n et m étant des entiers naturels).

Principe Additif : Si E et F sont disjoints, alors le nombre d'éllements de E ∪ F est n + m.

Principe Multiplicatif : Le produit cartésien de E et F noté E × F est l'ensemble des couples formés d'un élément de E et d'un élément de F. Le nombre d'éléments de E × F est n × m.

Attention : E × F et F × E sont généralement différents. Leurs éléments sont des couples similaires aux coordonnées d'un point (dans le plan).
Par conséquent, l'ordre a son importance.

Nombre de k-uplets : L'ensemble E × E × E peut être noté E3. C'est l'ensemble des 3-uplets (ou triplets) de E. Le nombre de triplets est n3.
Plus généralement, le nombre de k-uplets d'un ensemble de n éléments est nk.
On les note (e1 , e2 , ... , ek)

Partie d'un ensemble : Une partie de E est un sous-ensemble de E. Le nombre de parties de E est 2n.
E est une partie de lui-même. L'ensemble vide, noté ∅ contenant aucun élément est également une partie de E.
On note un ensemble E = {e1 , e2 , ... , ek} (mais ici, l'ordre n'a pas d'importance)

Factorielle d'un entier naturel : Le produit de tous les entiers naturels de 1 à n est appelé factorielle n. On la note n!.
n! = 1×2×3×...×n. (Par convention 0! = 1).

Nombre de k-uplets d'élements distincts : L'ensemble formé avec k éléments differents de E est l'ensemble des k-uplets d'élements distincts.
On parle parfois de k-arrangements. Le nombre d'éléments de cet ensemble est n×(n-1)×...×(n-(k-1)).
En utilisant les factorielles, on a : n × (n-1) × ... × (n-k+1) =     n!   
(n-k)!

Nombre de combinaisons : Une partie de k éléments d'un ensemble E formé de n éléments est appelé combinaison de k éléments de E.
On la note ( n
k		 ), on la lit k parmi n. Par convention ( 0
0		 ) = 1.
En utilisant les factorielles, on a : ( n
k		 ) =      n!    
k!(n-k)!		    Ainsi ( n
n-k		 ) =           n!         
(n-k)!(n-n+k)!		  =          n!       
(n-k)!(k)!		  = ( n
k		 )
Autres combinaisons utiles : ( n
0		 ) =      n!    
0!(n-0)!		  = 1 ; ( n
n		 ) =      n!    
n!(n-n)!		  = 1 et ( n
1		 ) =        n!      
1!(n-1)!		  = n 

Avec cette notation le nombre de parties d'un ensemeble de n éléments s'écrit : ( n
0		 ) + ( n
1		 ) + ... + ( n
n-1		 ) + ( n
n		 ) ou encore  Σ n
i=0		 ( n
i		 )
Or on a vu que ce nombre de parties était 2n. Par conséquent  Σ n
i=0		 ( n
i		 )  = 2n

Remarque : Les nombres ( n
k		 ), sont les coefficients binomiaux vus dans un autre chapitre... Anciennement noté C k
n

Triangle de Pascal

n \ k  0 1 2 3 4 5 6 7 8
0 1                
1 1 1              
2 1 2 1            
3 1 3 3 1          
4 1 4 6 4 1        
5 1 5 10 10 5 1      
6 1 6 15 20 15 6 1    
7 1 7 21 35 35 21 7 1  
8 1 8 28 56 70 56 28 8 1
On retrouve les coefficients observés lors du développement de (a + b )n...

Relation de Pascal : Si on considère deux entiers naturels n et k tels que 0 ≤ k ≤ n-1 alors :
      ( n
k		 ) + ( n
k+1		 ) = ( n+1
k+1		 )

* On peut démontrer cette relation par le calcul en utilisant l'expression donnée précédemment.
* Un autre méthode consiste à utiliser les combinatoires :

Pour cela on considère un ensemble E formé de n+1 éléments.
Le nombre de parties de E contenant k+1 éléments est ( n+1
k+1		 )

On cherche comment obtenir une partie de k+1 éléments de E.
Pour cela, on "isole" un élément de E. Deux cas sont alors possibles :
- l'élément est pris.
- l'élément n'est pas pris.

Dans le premier, pour avoir une partie de k+1 éléments de E,
il suffit de choisir en plus de l'élément "isolé", k éléments
parmi les n disponibles. Soit ( n
k		 )
Dans le second, il faut choisir les k+1 éléments parmi les n. Soit ( n
k+1		 )
D'après le principe additif, on donc : ( n+1
k+1		 ) = ( n
k		 ) + ( n
k+1		 )


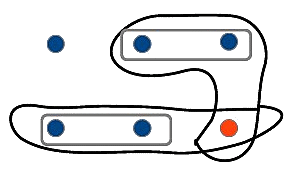triplets avec l'élément "isolé"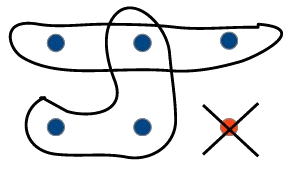

triplets sans l'élément "isolé"