Retour | Index | Suite

Orthogonalité dans l'espace

  • Deux vecteurs non nuls→u et→v sont dits orthogonaux si et seulement si,
    il existe deux droites sécantes perpendiculaires de vecteurs directeurs respectifs→u et→v.


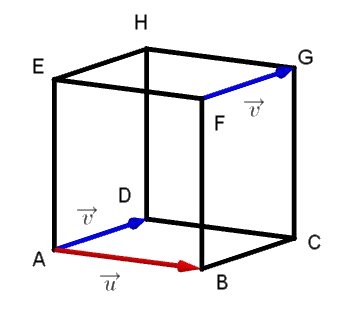
    Exemple : On considère un cube ABCDEFGH.
    Dans un cube, les vecteurs FG→et→AD sont égaux.
    Les droites (AB) et (AD) sont sécantes et perpendiculaires.
    Leurs vecteurs directeurs sont respectivement AB→et AD→=→FG.
    Par conséquent, les vecteurs AB→et FG→sont orthogonaux.

    Remarque : Les droites (AB) et (FG) sont orthogonales !
    On ne dit pas perpendiculaires car elles ne sont pas coplanaires.

  • Deux vecteurs non nuls→u et→v sont orthogonaux si et seulement si,→u.v→= 0.

  • Dans l'espace, le vecteur nul est orthogonal à tout vecteur.

    Expression dans un repère de l'espace

    Une base de l'espace est constituée de trois vecteurs non coplanaires.
    Un repère de l'espace sera constitué d'un point et d'une base de l'espace.
    Si les trois vecteurs sont deux à deux orthogonaux et que leurs normes sont toutes égales à 1, la base est dite orthonormée.
    Un repère avec une telle base sera dit repère orthonormé.

    Dans un repère (O ;→i ,→j ,→k) dire qu'un point a pour coordonnées M(x ; y ; z) signifie que le vecteur→OM = x×i→ + y×j→ + z×k→.
    Si on pose →u =→OM, les coordonnées du vecteur seront →u (x ; y ; z). Une écriture en colonne comme ci-après est possible.

    Dans un repère orthonormé, si on considère→u( x
    y
    z    		 ) et→v( x'
    y'
    z'    		 ) alors 
  • Le produit scalaire s'écrit :→u.v→= x × x' + y × y' + z × z'

  • Le carré scalaire s'écrit :→u.u→= x2 + y2 + z2 et par conséquent,
    →||u|| = √x2 + y2 + z2

  • Si →u = AB→avec A(xA ; yA ; zA) et B((xB ; yB ; zB)
    alors la distance AB = √(xB - xA)2 + (yB - yA)2 + (zB - zA)2

    • Orthogonalité de deux droites.

    Deux droites sont orthogonales si et seulement si leurs vecteurs directeurs sont orthogonaux.
    Et par conséquent si et seulement si le produit scalaire de ces deux vecteurs est nul.

    Si les deux droites sont (en plus) coplanaires on dit alors qu'elles sont perpendiculaires.
    (Elles sont alors sécantes.)

    Remarques : Pour définir une droite, il suffit de deux points ou d'un point et d'un vecteur.
    Deux droites parallèles ont même vecteur directeur.

    Orthogonalité d'une droite et d'un plan.

    Une droite est orthogonale à un plan si et seulement si un vecteur directeur de cette droite est orthogonal à deux vecteurs non colinéaires du plan.
    Par conséquent, la droite sera orthogonale à toutes les droites du plan, ou à deux droites sécantes du plan.

    Il n'existe qu'une seule droite passant par un point et orthogonale à un plan.
    Il n'existe qu'un seul plan passant par un point et orthogonal à une droite.

    Un vecteur normal à un plan est un vecteur directeur d'une droite orthogonale au plan.

    Si A est un point de l'espace et→n un vecteur non nul, l'unique plan passant par A et de vecteur normal→n,
    est l'ensemble des points M tels→AM.n→= 0.

    Remarques : Pour définir un plan, il suffit de trois points non alignés ou d'un point et de deux vecteurs non colinéaires.
    Deux vecteurs non colinéaires constituent une base du plan.

    Projeté orthogonal.

    Le projeté orthogonal d'un point sur une droite est le point d'intersection de cette droite et de la droite perpendiculaire passant par le point.
    (si le point est sur la droite le projeté est lui-même).

    Le projeté orthogonal d'un point sur un plan est le point d'intersection de ce plan et de la droite perpendiculaire passant par le point.
    (si le point est dans le plan le projeté est le point lui-même).

    Remarque : La distance entre un point et son projeté orthogonal sur une droite ou un plan, est la plus court distance du point à la droite ou au plan.