Index | Suite

Vecteurs dans l'espace

La plupart des définitions et des propriétés sont les mêmes dans le plan et dans l'espace...

Définitions et propriétés

  • Un vecteur est caractérisé par sa norme, son sens et sa direction.
  • Si A et B sont deux points distincts de l'espace, le vecteur →AB est caractérisé par :
    - sa norme notée ||AB||→
    - sa direction, celle de la droite (AB)
    - son sens, celui de A vers B.

    Ainsi, à partir d'un point, il n'existe qu'un seul point tel que le vecteur formé par ces deux points soit égal à un vecteur donné.

    Si on considère un vecteur→AB et un point C, la translation de vecteur→AB (qui transforme A en B),
    transforme C en D si et seulement si →AB =→CD.
    Cette égalité est une des caractéristiques d'un parallélogramme.

    →AB = CD→⇔  ABDC est un parallélogramme ou ABCD est un parallélogramme  ⇔→AB = DC→.
    Attention à l'ordre des lettres ! Dans le doute faire un schéma...

    Remarque : Si →AB et CD→sont colinéaires, les droites (AB) et (CD) sont parallèles.
    Le quadrilatère ABDC est un trapèze.

    Somme de vecteurs
    Pas de changement par rapport à ce qui se passe dans le plan...

    La somme de deux vecteurs→u et v→est un vecteur noté→u + v→

    La relation de Chasles s'écrit toujours :→AB + BC→= →AC.

    On peut également rappeler une autre définition d"un parallélogramme :
    →AB + AD→=→AC  ⇔  ABCD est un parralélogramme..

    Produit d'un vecteurs par un réel
    Le produit d'un vecteur→u par un réel k est un vecteur noté ku→
    - la norme du vecteur ||ku||→= |k| × ||u||→ - les deux vecteurs →u et ku→ont même direction
    - si k > 0 les deux vecteurs ont même sens et si k < 0 les deux vecteurs sont en sens contraire.

    Cette propriété traduit la colinéarité de deux vecteurs.
    Deux vecteurs→u et v→sont colinéaires si et seulement si il existe un réel k tel que →v = k×u→

    Remarque : Si A, B et C sont trois points distincts de l'espace.
    Si par exemple les vecteurs→AB et AC→sont colinéaires alors les points sont alignés.

    • Combinaisons linéaires de vecteurs
    En regroupant la somme et le produit par un réel, on définit une combinaison linéaire.

    On dit qu'un vecteur→w et une combinaison linéaires des vecteurs→u et →v,
    s'il existe deux réels a et b tels que :→w = a×u→+ b×v→.

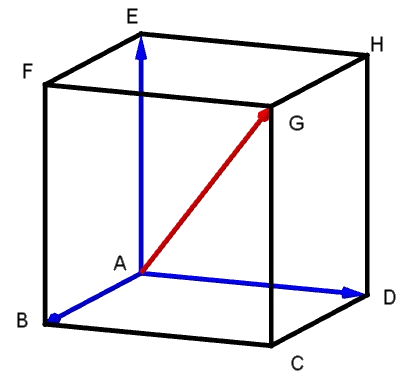
    Les combinaisons ne sont pas limitées à deux termes.
    On peut les généraliser avec 3, 4 ou plus de vecteurs...

    Exemple : Dans un cube ou dans un parallélépipède rectangle ABCDEFGH on a :
    →AG  =  AB→+→AD  +→AE.
    En effet, en utilisant la relation de Chasles :
    →AG  =  AB→+→BC  +→CG. Or →BC  =  AD→ et →CG  =→AE.

    Vecteurs coplanaires

    Des vecteurs sont coplanaires si et seulement si,

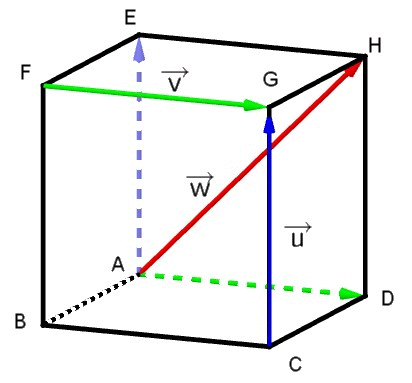
  • il existe des représentants de ces vecteurs dans un même plan.

  • il existe une combinaison linéaires donnant l'un en fonction des autres.

    Exemple : Dans un cube ABCDEFGH on considère :
    →u = CG→;→v = FG→et→w = AD→.

  • On a : CG→=→AE et FG→=→AD.
    Les vecteurs→AE, →AD et →AH sont dans le même plan.
    Par conséquent, les vecteurs→u,→v et→w sont coplanaires.

  • On a : AH→=→AD + DH→ Or AD→=→FG et DH→=→CG
    Donc AH→=→FG + CG→; Par conséquent, il existe une combinaison linéaires
    donnant l'un en fonction des deux autres.
    Les vecteurs→u,→v et→w sont coplanaires.