Manipulation dans l'espace

Droites dans l'espace

Définitions et propriétés

Par deux points distincts de l'espace passe une et une seule droite.

Le vecteur formé par ces deux points est un vecteur directeur de la droite.
Tout vecteur non nul dont la direction est la même que celle de la droite est un vecteur directeur de cette droite.

Si A et B sont deux points distincts de l'espace, la droite (AB) est l'ensemble des points M tel que →AM = k×AB→ où k est un réel.
Autrement dit, la droite (AB) est l'ensemble des points M tel que les vecteurs→AM et AB→sont colinéaires.

Il existe une et une seule droite passant par un point de l'espace et parallèle à une droite donnée.
On peut définir une droite par un seul point et son vecteur directeur.

Les droites ayant même vecteur directeur sont parallèles (ou confondues).

Deux droites peuvent être coplanaires (incluses dans le même plan). Elles peuvent alors être :
- sécantes en un point (leurs vecteurs directeurs ne sont pas colinéaires). (elles peuvent être perpendiculaires).
- strictement parallèles (leurs vecteurs directeurs ne sont pas colinéaires ; aucun point commnun).
- confondues (leurs vecteurs directeurs ne sont pas colinéaires ; Un point commnun, donc tous).

Deux droites peuvent être non coplanaires. Elles n'ont pas de point commun.
- elle peuvent être strictement parallèles (leurs vecteurs directeurs ne sont pas colinéaires).
- elle peut aussi être orthogonales (vecteurs directeurs orthogonaux).
- "quelconques" ni parallèles ni orthogonales.

Positions relatives d'une droite et d'un plan
Une droite peut être :
- sécante au plan (son vecteur directeur et deux vecteurs non colinéaires du plan sont coplanaires);
il existe alors une combinaison linéaire reliant les 3 vecteurs)
- strictement parallèle au plan (les 3 vecteurs sont linéairement indépendants).
- incluse dans le plan.

Plans dans l'espace

Définitions et propriétés

Par trois points non alignés de l'espace passe un et un seul plan.

Deux vecteurs formés à partie de ces points sont des vecteurs directeurs du plan.
Les points n'étant pas alignés les vecteurs ainsi formés ne sont pas colinéaires.
Tout vecteur du plan peut s'exprimer comm une combinaison linéaires des deux vecteurs.

Si A, B et C sont trois points non alignés de l'espace, le plan (ABC) est l'ensemble des points M tel que
→AM = x×AB→ + y×AC→ où x et y sont des réels.
Autrement dit, le plan (ABC) est l'ensemble des points M tel que les vecteurs→AM, AB→et AC→sont coplanaires.

Il existe un et un seul plan passant par un point de l'espace et parallèle à un plan donné.
On peut définir un plan par un seul point et deux vecteurs non colinéaires.

Positions relatives des deux plans
Deux plans peuvent être:
- sécants (Ils se coupent selon une droite). (ils peuvent être orthogonaux)
- strictement parallèles (leurs vecteurs bases sont égaux).
- confondus (parallèles avec un point commnun, donc tous).

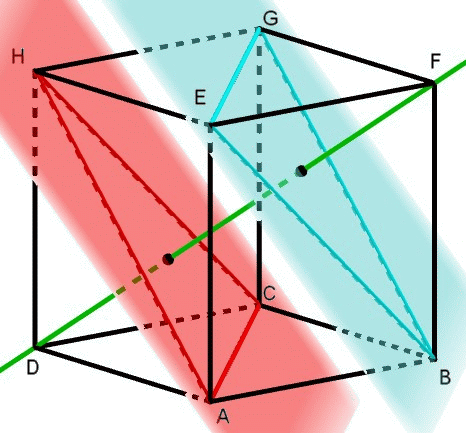
Exemple : Dans un cube ABCDEFGH les plans (ACH) et (BEG) sont parallèles.
En effet,→AH et AC→sont des vecteurs de la base du plan (ACH).
→BG et EG→sont des vecteurs de la base du plan (BEG).
Les cotés des triangles ACH et BEG sont des diagonales des faces du cubes. On peut montrer que →AH = BG→ et→AC = EG→.
Ainsi, deux vecteurs non colinéaires du plan (ACH) sont égaux à deux vecteurs non colinéaires du plan (BEG).
Les plans sont donc parallèles.

On peut également montrer que la droite (DF) est orthogonale à ces plans. On exprime les vecteurs en fonction de→AB, AD→ et→AE.
On calcule les produits scalaires...