Bases et repères de l'espace

Une base de l'espace est constituée de trois vecteurs non coplanaires.

Un repère de l'espace sera constitué d'un point et d'une base de l'espace.

Si les trois vecteurs sont deux à deux orthogonaux et que leurs normes sont toutes égales à 1, la base est dite orthonormée.
Un repère avec une telle base sera dit repère orthonormé.

Dans un repère (O ;→i ,→j ,→k) dire qu'un point a pour coordonnées M(x ; y ; z) signifie que le vecteur
→OM = x×i→ + y×j→ + z×k→. On appelle x l'abscisse, y l'ordonnée et z la côte.
Si on pose →u =→OM, on définit les coordonnées du vecteur→u (x ; y ; z). Une écriture en colonne est possible.

On considère deux vecteurs dans ce repère. On a→u (x ; y ; z) et→v (x' ; y' ; z').
- Deux vecteurs sont égaux si ils ont mêmes coordonnées : →u = v→ ⇔ x = x', y= y' et z = z'.
- Les coordonnées de la somme de deux vecteurs→u + v→sont  (x + x' ; y + y' ; z + z').
- Les coordonnées du produit d'un vecteur par un réel k, noté k×u→sont  (k×x ; k×y ; k×z).

Dans un repère (O ;→i ,→j ,→k), On considère deux points distincts de coordonées A(x_A ; y_A ; z_A) et B((x_B ; y_B ; z_B)
D'après la relation de Chasles,→AB =→AO + OB→=→OB - OA→ = x_Bi→ + y_Bj→ + z_Bk→ - (x_Ai→ + y_Aj→ + z_Ak→)
D'où→AB = (x_B - x_A)×i→ + (y_B - y_A)×j→ + (z_B - z_A)×k→
- Les coordonnées du vecteur→AB sont (x_B - x_A ; y_B - y_A ; z_B - z_A)

Si le point I est le milieu du segment [AB] alors→AI =

1 2

×AB→.

De plus→OI =→OA +→AI = →OA +

1 2

×(OB→-→OA) =

1 2

×(OA→+→OB).

- Les coordonnées du milieu du segment [AB] sont (

xA + xB     2

;

yA + yB     2

;

zA + zB     2

).

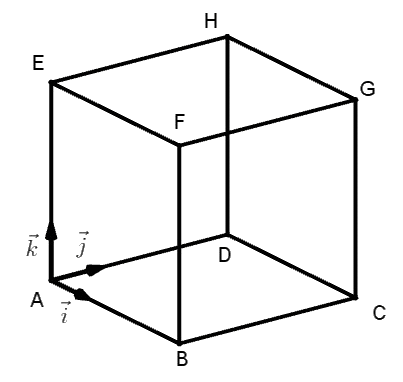
Exemple : On considère un cube ABCDEFGH d'arrête 1. Les point A, B, D et E ne sont pas dans le même plan (coplanaires). Les vecteurs,→AB et AD→et→AE forme une base de l'espace. On peut alors définir le repère orthonormé d'origine A : (A ;→AB ,→AD ,→AE). Dans ce repère, un point M(x ; y ; z) est tel que→AM = x×AB→+y×AD→+z×AE→. Les coordonnées de tous les points sont : A(0 ; 0 ; 0) ; B(1 ; 0 ; 0) ; D(0 ; 1 ; 0) ; E(0 ; 0 ; 1) ; C(1 ; 1 ; 0) ; F(1 ; 0 ; 1) ; G(1 ; 1 ; 1) et H(0 ; 1 ; 1). →AC = AB→+ BC→ = AB→+ AD→car dans un cube→BC = AD→ soit→AC = 1×AB→+ 1×AD→+ 0×AE→d'où les coordonnées... Remarque 1 : Si l'arrête est un réel a ≠ 1, on peut toujours définir un repère orthonormé d'origine A. Il suffit de choisir trois vecteurs →i,→j  et→k tels que : →AB = a×i→, →AD = a×j→ et →AE = a×k→. Les coordonnées des points sont : A(0 ; 0 ; 0) ; B(a ; 0 ; 0) ; D(0 ; a ; 0) ; E(0 ; 0 ; a)...

Remarque 2 : Pour un pavé droit (parallélépidèpe rectangle) ABCDEFGH d'arrêtes
a = AB, b = AD et c = AE, on peut définir un repère orthonormé (A;→i,→j  et→k) avec:
→AB = a×i→, →AD = b×j→ et →AE = c×k→.
Les coordonnées des points sont : A(0 ; 0 ; 0) ; B(a ; 0 ; 0) ; D(0 ; b ; 0) ; E(0 ; 0 ; c) ;
C(a ; b ; 0) ; F(a ; 0 ; c) ; G(a ; b ; c) et H(0 ; b ; c).