|
Recherche d'un volume minimal
Problème 2 : Cône circonscrit à une sphère.
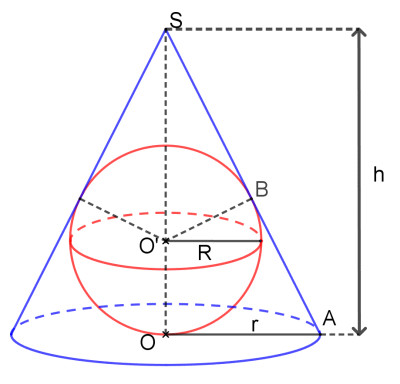
Soit une sphère de centre O' et de rayon R. On souhaite inscrire cette sphère dans un cône dont le volume est le plus petit possible.
On désigne par h la hateur OS du cône et par r le rayon du disque de sa base. On a O' ∈ [OS] et on pose O'S = x.
Remarque : La sphère est tangente au cône en O et en B.
1. On a x = h - R. Pour quelles valeurs de h et x le cône peut-il être construit ?
| 2. Montrer que r2 = R2× |
x + R
x - R |
| 3. En déduire que V(h) = |
Π R2
3 |
× |
h2
h - 2R |
4. Calculer la dérivée V'(h) et étudier les variations de V(h) sur ]2R ; +∞[.
5. Pour quelle valeur de h le volume est-il minimum ?
|
|
|
1. Pourque le cône puisse être construit il faut que sa hauteur soit strictement supérieur au diamètre de la sphère.
Soit h > 2R soit encore h ∈ ]2R ; +∞[ ou x ∈ ]R ; +∞[ .
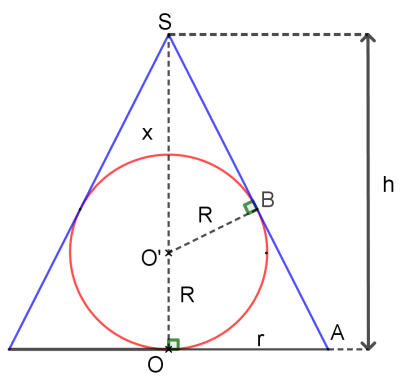
2. La sphère est tangente à la surface latérale du cône en B. Or la tangente à un cercle (ou à une sphère) est une droite perpendiculaire au rayon.
Les droites (O'B) et (SB) sont donc perpendiculaire et le triangle BSO' est rectangle en B.
Par ailleurs, la hauteur OS est perpendiculaire à la base du cône donc ASO est un triangle rectangle en O.
On note α le demi-angle au sommet de cône.
|
|
|
|
| Dans le triangle BSO' on peut écrire sin(α) = |
BO'
SO' |
= |
R
x |
donc sin2(α) = |
R2
x2 |
| Dans le triangle ASO, d'une part, sin(α) = |
OA
SA |
= |
r
SA |
et sin2(α) = |
r2
SA2 |
d'autre part, d'après le théorème de Pythagore on a SA2 = OA2 + OS2 = r2 + (x + R)2.
| On a alors : |
R2
x2 |
= |
r2
r2 +(x + R)2 |
Soit R2×(r2 + (x + R)2) = r2×x2 |
En regroupant les termes en r2, on obtient :
R2(x + R)2 = r2×(x2 - R2) ⇔ R2(x + R)2 = r2×(x - R)(x + R)
⇔ R2(x + R) = r2×(x - R)
| D'où l'expression suivante : r2 = R2× |
x + R
x - R |
| 3. Le volume d'un cône est V(h) = |
1
3 |
×Πr2×h, de plus x = h - R |
| Par conséquent V(h) = |
1
3 |
Π×R2× |
h - R + R
h - R - R |
×h = |
Π R2
3 |
× |
h
h - 2R |
×h = |
Π R2
3 |
× |
h2
h - 2R |
Calculer la dérivée V'(h) et étudier les variations de V(h) sur ]2R ; +∞[.
| 4. On pose f(h) = ah2 et g(h) = h - 2R, avec a = |
Π R2
3 |
| f'(h) = 2ah et g'(h) = 1. |
|
|
| V = |
f
g |
donc V' = |
f'g - fg'
g2 |
|
| D'où V'(h) = |
2ah(h - 2R) - ah2
(h - 2R)2 |
= |
ah(2h - 4R - h)
(h - 2R)2 |
= |
ah(h - 4R)
(h - 2R)2 |
V'(h) = 0 pour h = 0 et h = 4R et V'(h) < 0 (signe de -a) entre les racines.
| |
2R |
|
4R |
|
+∞ |
| signe de V'(x) |
|
- |
0 |
+ |
|
variation
de V(h) |
|
↘ |
|
↗ |
|
| |
V(4R) |
|
|
5. D'après le tableau des variations de V(h) le volume du cône est minimal pour h = 4R.
| Et V(4R) = |
Π R2
3 |
× |
(4R)2
4R - 2R |
= |
Π R2
3 |
× |
16R2
2R |
= |
8 Π R3
3 |
|

