Fonctions Affines et Linéaires

On considère les fonctions définies sur IR par g(x) = ax + b.

Si a = 0, la courbe représentive de la fonction est une droite parallèle à l'axe des abscisses.
La fonction est constante. L'équation réduite de la droite est y = b.

Si b = 0, la courbe représentive de la fonction est une droite passant par l'origine du repère. La fonction est linéaire.
L'équation réduite de la droite est y = ax.

Si a ≠ 0 et b ≠ 0, La fonction est affine, Sa courbe représentive de la fonction est une droite passant par le point de coordonnées (0 ; b).
b est appelé ordonnées à l'origine et a est le coefficient directeur. L'équation réduite de la droite est y = ax + b.

Une droite parallèle à l'axe des ordonnées ne représente pas une fonction, mais une équation du type x = k peut être écrite (k est l'abscisse de tous les points de la droite).

Soient u et v deux nombres réels tels que u > v c'est à dire tels que u - v > 0.
g(u) - g(v) = a.u + b - (a.v + b) = a.u + b - a.v - b = a.u - a.v = a(u - v).
On sait que u - v est positif donc le signe de g(u) - g(v) est donné par le signe du coefficient directeur a.
Il en résulte que les fonctions affines (ou linéaires) sont croissantes si a > 0
et décroissantes si a < 0.

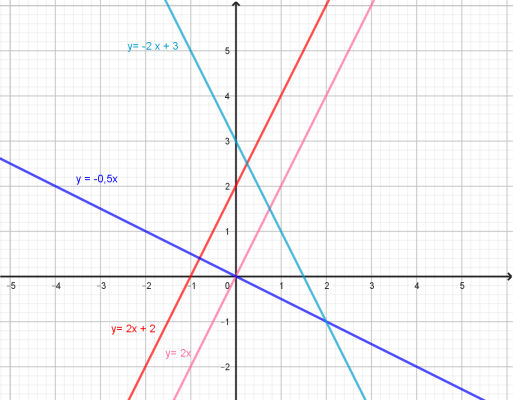Ci-contre les représentations graphiques des fonctions affines : 2x + 2 et -2x + 3 et des fonctions linéaires : 2x et -0,5x Remarque : Deux droites parallèles ont le même coefficient directeur.

Si a ≠ 0, g(x) = 0 pour x = -b/a et g(x) > 0 ⇔ ax + b > 0 ⇔ ax > -b
Si a > 0 alors ax > -b ⇔ x > -b/a (multiplier ou diviser par un nombre positif ne change pas le sens des inégalités)
Si a < 0 alors ax > -b ⇔ x < -b/a (multiplier ou diviser par un nombre positif change le sens des inégalités)

On peut résumer tout ceci par le tableau des signes suivant :

signe de	-∞		-b/a		+∞
ax + b		signe de -a	0	signe de a