|
Définition
Si on considère deux vecteurs non nuls→u et→v, le produit scalaire de→u par→v est le nombre réel
noté→u.v→(on dit→u scalaire v→) défini par
→u.v→=→∥u∥ × ∥v∥→× cos(u→,→v)
où→∥u∥ et ∥v∥→sont les normes des vecteurs→u et→v c'est-à-dire leur longueurs.
Dans le cas où→v =→u, on a→u.u→=→∥u∥2.
On note ce nombre→u2 et on l'appelle carré scalaire de→u.
Autres définitions
Si on considère trois points distincts A, B et C tels que→AB =→u et→AC =→v on aura :
→AB.AC→= AB × AC × cos(AB→,→AC) soit encore
→AB.AC→= AB × AC × cos(BAC)^
Si le point H désigne le projeté orthogonal du point C sur la droite (AB), on obtient l'expression :
→AB.AC→=-AB × AH-où-AB et AH-sont les mesures algébriques.
Si les vecteurs→AB et→AH sont dans le même sens alors :
→AB.AC→= AB × AH |
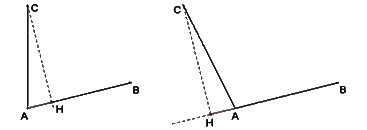 |
Si les vecteurs→AB et→AH sont de sens opposés alors :
→AB.AC→= - AB × AH |
| Dans un repère orthonormal (orthonormé), si on considère→u( |
x
y |
) et→v( |
x'
y' |
) alors |
le produit scalaire s'écrit :→u.v→= x × x' + y × y'
|
|
Propriétés
Soient→u,→v et→w trois vecteurs non nuls. Soient k un réel non nul.
→u.v→=→v.u→
|
Le produit scalaire est symétrique
|
→u.( kv→) = k ×→u.v→
→u.(v→+→w) = →u.v→+→u.w→
( ku→). v→ = = k ×→u.v→
(u→+→v). w→= →u.w→+→v.w→
|
Le produit scalaire est linéaire
On dit également bilinéaire car
"linéaire à droite" et "linéaire à gauche"
|
Autres expressions
Si on considère deux vecteurs non nuls→u et→v alors on peut écrire les égalités remarquables suivantes :
(u→+→v)2 = →u2 + 2→u.v→+→v2
(u→-→v)2 = →u2 - 2→u.v→+→v2
(u→+→v)(u→-→v) = →u2 -→v2
Ainsi on en déduit les expressions du produit scalaire :
| →u.v→= |
1
2 |
(∥u→+→v∥2 -→∥u∥2 -→∥v∥2) |
et →u.v→= |
1
2 |
(→∥u∥2 +→∥v∥2 - ∥u→-→v∥2) |
Si on considère trois points distincts A, B et C tels que→AB =→u et→AC =→v la seconde expression devient :
| →AB.AC→= |
1
2 |
(AB2 + AC2 - BC2) |
|
