Calcul d'angles et de longueurs
formule d'Al Kashi
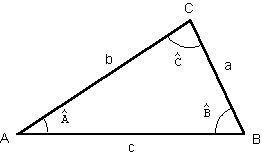
On considère un triangle ABC non aplati.
On pose BC = a, AC = b et AB = c et on note
^A l'angle BAC^,^B l'angle ABC^et^C l'angle ACB^.
|
 |
On reprend les expressions vues précédemment :
→AB.AC→= AB × AC × cos(BAC)^et
| →AB.AC→= |
1
2 |
(AB2 + AC2 - BC2) |
|
En utilisant les notations de la figure, on peut écrire 2×c×b×cos(A)^= c2 + b2 - a2
Soit encore a2 = c2 + b2 - 2×c×b×cos(A)^ (formule d'Al Kashi).
Par rotation des variables on obtient :
b2 = a2 + c2 - 2×a×c×cos(B)^et c2 = b2 + a2 - 2×b×a×cos(C)^
Remarque : Si l'angle est de 90°, on retrouve le théorème de Pythagore.
formule des sinus
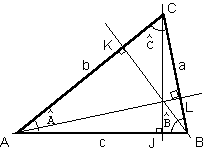
Dans un triangle ABC, les hauteurs issues des trois sommets peuvent s'exprimer de deux mannières.
Pour la hauteur issue de C, en considérant les triangles ACJ et BCJ rectangles en J
on a d'une part CJ = b × sin(A)^ et d'autre part CJ = a × sin(B)^. On a donc :
| b × sin(A)^= a × sin(B)^ que l'on peut écrire |
b
sin(B)^ |
= |
a
sin(A)^ |
Pour la hauteur issue de B, en considérant les triangles ABK et BCK rectangles en K
on arrive à :
|
 |
| BK = c × sin(A)^= a × sin(C)^ que l'on peut écrire |
c
sin(C)^ |
= |
a
sin(A)^ |
|
|
En considérant les triangles ABL et ACL rectangles en L, la hauteur issue de A conduit à :
| AL = c × sin(B)^= b × sin(C)^ soit |
c
sin(C)^ |
= |
b
sin(B)^ |
| On peut donc résumer ces égalités par la relation : |
a
sin(A)^ |
= |
b
sin(B)^ |
= |
c
sin(C)^ |
|
Théorème de la médiane
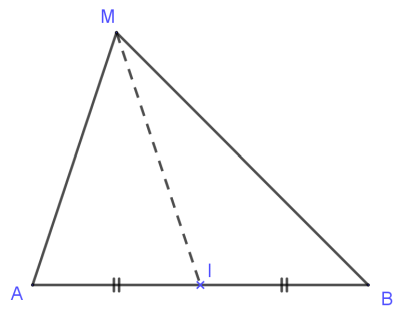
On considère un triangle AMB et le point I milieu du segment [AB]. La droite (MI) est donc la médiane issue de M.
On cherche alors une expression "simple" du produit scalaire→MA.MB→.
En utilisant de la relation de Chasles on peut écrire :
| →MA.MB→= |
(MI→+→IA).(MI→+→IB) |
|
| = |
→MI.MI→+→MI.IB→+→IA.MI→+→IA.IB→ |
| = |
→MI2 +→MI.IB→+→MI.IA→+→IA.IB→
(car→u.v→=→v.u→) |
| = |
MI2 +→MI.(IB→+→IA) +→IA.IB→
|
| = |
MI2 +→MI.0→+→IA.IB→
(car →IB + IA→= 0→) |
| = |
MI2 + 0 - | →AB
2 | . | AB→
2 |
(car →IB = - IA→= | →AB
2 | ) |
Vecteur normal à une droite
Un vecteur directeur d'une droite d'équation cartésienne ax + by + c = 0 est
| →u( |
-b
a |
) un vecteur normal à cette droite sera→n( |
a
b |
). Les équations cartésiennes |
des droites perpendiculaires seront de la forme -bx + ay + c' = 0 (ou bx - ay + c' = 0).
| Autrement dit si →u( |
a
b |
) est un vecteur directeur d'une droite D |
| alors →n( |
-b
a |
) ou →n( |
b
-a |
) est un vecteur normal à cette droite. |
En effet, →u.n→= a×(-b) + b×a = -ab + ba = 0 (ou →u.n→= a×b + b×(-a) = ab - ba = 0 )
|


