Retour | Index | Suite

Applications du produit scalaire

Détermination d'un ensemble de points

  • Ensemble des points tels que →MA.MB→= k

    On a vu que d'après le théorème de la médiane que→MA.MB→=  MI2 - AB2
    4    		  
    →MA.MB→= k ⇔  MI2 - AB2
    4    		  = k ⇔ MI2 =  k + AB2
    4

    ◊ Si k + AB2/4 = 0, la seule solution au problème est le point I

    ◊ Si k + AB2/4 < 0, le problème n'a pas de solution.

    ◊ Si k + AB2/4 > 0,l'ensemble des points recherchés est
    le cercle de centre I et de rayon √k + AB2/4.

  • Ensemble des points tels que →AM.AB→= k

    ◊ Si k = 0
    On a→AM.AB→= 0. Les deux vecteurs sont orthogonaux et par conséquent les droite (AM) et (AB) sont perpendiculaires.
    L'ensemble des points recherchés est la droite Δ perpendiculaire à la droite (AB) passant par A.

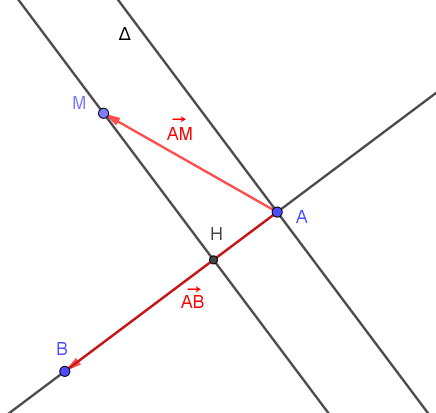
    ◊ Si k > 0
    On a→AM.AB→> 0. Les vecteurs sont "plutôt" dans le même sens. L'angle en^A est entre 0 et 90°. L'angle orienté→(AM,AB)→est compris entre -π/2 et π/2. Si on considère la droite Δ perpendiculaire à (AB) passant par A, M est dans le demi-plan contenant B.
    Le projeté orthogonal de M sur la droite (AB) est alors sur la demi-droite [AB).
    →AM.AB→=→AH.AB→= AH × AB
    →AM.AB→= k ⇔ AH × AB = k ⇔ AH = k/AB
    On peut se ramener à une égalité vectorielle en considérant un vecteur unitaire de même sens que→AB. Un tel vecteur peut être obtenu en divivant le vecteur→AB par sa norme AB.
    Ainsi on peut écrire : AH→=   k 
    AB    		 ×  AB→
    AB    		  =   k 
    AB2    		 →AB
    L'ensemble des points recherchés est la droite perpendiculaire à la droite (AB) passant par H.

    		•  

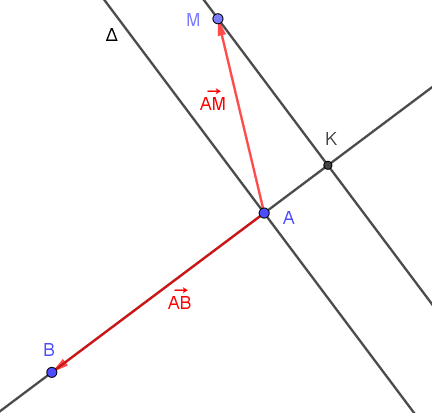
    ◊ Si k < 0
    On a→AM.AB→< 0. Les vecteurs sont "plutôt" de sens contraire. L'angle en^A est supérieur à 90° (mais inférieur à 270°). L'angle orienté (→AM,AB→) est compris entre -π et -π/2 ou entre &pi/2; et π. Si on considère la droite Δ perpendiculaire à (AB) passant par A, M est dans le demi-plan ne contenant pas B.
    Si on appelle K le projeté orthogonal de M sur la droite (AB), on a le point A appartenant au segment [KB].
    →AM.AB→=→AK.AB→= - AK × AB
    →AM.AB→= k ⇔ - AK × AB = k ⇔ AH = -k/AB
    En utilisant le vecteur unitaire obtenu en divivant le vecteur→AB par sa norme AB, on a :
    AK→=   k 
    AB    		 ×  AB→
    AB    		  =   k 
    AB2    		 →AB (car k est négatif !)
    L'ensemble des points recherchés est la droite perpendiculaire à la droite (AB) passant par K.

    Remarques : On peut rencontrer des variantes à ce type de problème.
    →MA.AB→= k ; →AM.BA→= k voire →MA.BA→= k.

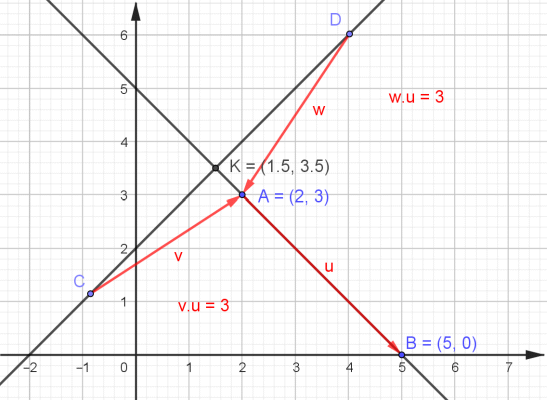
    Exemple : Dans un repère orthonormé (O ;→i,→j), on considère les points A(2;3) et B(5;0).
    Déterminer l'ensemble des points M tels que :→MA.AB→= 3.
    Méthode 1 :→MA.AB→= -→AM.AB→ car →MA = -→AM. Par conséquent →MA.AB→= 3 ⇔ →AM.AB→= -3
    On est donc dans le cas k < 0 ci-dessus.
    L'ensemble des points est donc la droite (d) perpendiculaire à (AB) passant par le point K tel que
    AK→=   -3 
    AB2    		 →AB =  -1 
    6    		 →AB.
    Car→AB(3;-3) et AB2 = 32 + (-3)2 = 18
    On peut en déduire K(3/2;7/2), ainsi qu'une équation cartésienne de la droite (d).
    En effet, M(x;y)∈(d) ⇔ →AB.KM→= 0
    ⇔ 3×(x-3/2) - 3×(y-7/2) = 0
    ⇔ 3x - 9/2 - 3y + 21/2 = 0
    ⇔ 3x - 3y + 12/2 = 0 ⇔ x - y + 2 = 0
    Méthode 2 :On considère M(x;y), d'où →MA(2-x;3-y). De plus→AB(3;-3)
    Donc →MA.AB→= 3 ⇔ (2-x)×3 + (3-y)×(-3) = 3 ⇔ 6 -3x - 9 + 3 y = 3
    ⇔ -3x - 3 + 3 y - 3 = 0 ⇔ x - y + 2 = 0 (en divisant par -3).

  • Autres expressions utiles.

    ◊ MA2 + MB2 =  MI2 +  AB2
    2    		   avec I milieu de [AB]

    ◊ MA2 - MB2 = 2→MI.BA→ avec I milieu de [AB]