Retour | Index

Signe d'un polynôme du second degré

Mise en évidence

On reprend le polynôme du second degré sous la forme:
p(x) = a[(x - α)2 -   Δ 
4a2		 ]  avec Δ = b2 - 4ac
Si Δ < 0, l'expression entre crochets est strictement positive.
Le signe de p(x) est donné par le signe de a quelque soit la valeur de x.

Si Δ = 0 , p(x) = a(x - α)2 et un carré est toujours positif ou nul.
Le signe de p(x) est donné par le signe de a en tout point sauf pour x = α où p(x) = 0.

Si Δ > 0 , p(x) = a(x - x1)(x - x2). De plus, x - x1 > 0 ⇔ x > x1 et x - x2 > 0 ⇔ x > x2.
On suppose que x1 < x2 et on dresse le tableau des signes de (x -x1)(x -x2).
signe de -∞   x1   x2   +∞
(x - x1)   -  0 +  ¦ +   
(x - x2)   -  ¦ -  0 +   
 (x - x1)(x - x2)    +  0 -  0 +   
Le signe de p(x) est donné par le signe de -a entre les racines et par le signe de a à l'extérieur des racines.

Signe d'un polynôme du second degré p(x) = ax2 + bx + c

Δ < 0 -∞   +∞
 signe de p(x)    signe de a  

Δ = 0 -∞   -b/2a   +∞
 signe de p(x)    signe de a 0 signe de a  

Δ > 0 -∞   x1   x2   +∞
 signe de p(x)    signe
de a		 0 signe
de -a		 0 signe
de a		  
  
Excercice : Soit la fonction définie par f(x) = x3 - 2x2 - x + 2.
1. Vérifier que 1 est une racine de l'équation f(x) = 0 .
On calcule f(x) pour x  = 1 ; f(1) = 13 -2×12 - 1 + 2 = 1 - 2 + 1 = 0.
1 est bien une racine de l'équation f(x) = 0.

2. Trouver les réels a, b et c tels que f(x) = (x - 1)(ax2 + bx + c).
On developpe l'expression donnée et on regroupe les coefficients de même puissance de x
f(x) = (x - 1)(ax2 + bx + c) 
     = ax3 + bx2 + cx - ax2 - bx - c.
     = ax3 + (b -a)x2 + (c - b)x - c.




On identifie ces coefficients avec ceux de f(x). On obtient un système de 4 équations 
à 3 inconnes (une des équations ne sert qu'à vérifier l'exactitude des valeurs trouvées).






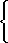a = 1
b-a = -2
c-b = - 1
-c = 2		
D'où

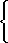a = 1
b = -1
c = -2		








3. Résoudre f(x) < 0.
D'après la question précédente f(x) = (x - 1)(x2 - x - 2).
On cherche les racines du polynôme du second degré.
Δ = (-1)2 - 4×1×(-2) = 1 + 8 = 9 = 32 ; Δ > 0 donc il y a deux racines distinctes




x1 = 
1 - 3
2		
 = -1 et x2 = 
1 + 3
2		
 = 2 ; 



Le coefficient de x2 étant positif, le polynôme est négatif sur ]-1 ; 2[.
On dresse le tableau des signes de f(x)




signe de
-∞
 
-1
 
1
 
2
 
+∞




(x - 1)
 
-
¦
-
0
+
¦
+
 




(x2 - x - 2)
 
+
0
-
¦
-
0
+
 




 (x - 1)(x2 - x - 2) 
 
-
0
+
0
-
0
+
 




L'ensemble des solutions de l'inéquation f(x) < 0 est S = ]-∞ ; -1[∪]1 ; 2[