|
Exercice 1 : Soient les suites U et V telles que pour tout n ∈ ℕ :
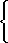 |
Un+1 = 3Un + 2Vn |
et |
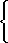 |
U0 = 1 |
| Vn+1 = 2Un + 3Vn |
V0 = 2 |
1. Calculer U1, V1, U2, V2, U3, V3.
U1 = 3U0 + 2V0 = 3×1 + 2×2 = 7
U2 = 3U1 + 2V1 = 3×7 + 2×8 = 21 + 16 = 37
U3 = 3U2 + 2V2 = 3×37 + 2×38 = 111 + 76 = 187 |
|
V1 = 2U0 + 3V0 = 2×1 + 3×2 = 8
V2 = 2U1 + 3V1 = 2×7 + 3×8 = 14 + 24 = 38
V3 = 2U2 + 3V2 = 2×37 + 3×38 = 74 + 114 = 188 |
2. On définit les suites X et Y par : Xn = Un + Vn et Yn = Un - Vn.
a. Montrer que X est une suite géométrique et que Y est une suite constante.
Xn+1 = Un+1 + Vn+1
Xn+1 = 3Un + 2Vn + 2Un + 3Vn
Xn+1 = 5Un + 5Vn
Xn+1 = 5(Un + Vn)
Xn+1 = 5Xn
|
et |
Yn+1 = Un+1 - Vn+1
Yn+1 = 3Un + 2Vn - 2Un - 3Vn
Yn+1 = Un - Vn
Yn+1 = Yn
|
Pour tout n on a : Xn+1 = qXn avec q = 5 et Yn+1 = Yn
Donc la suite X est géométrique et la suite Y est constante.
b. En déduire les formes explicites des suites X et Y.
X0 = U0 + V0 = 3 et Y0 = U0 - V0 = -1.
La suite X est une suite géométrique donc sa forme explicite est : Xn = X0×qn = 3×5n
La suite Y est constante donc Yn = Y0 = -1
3. Exprimer Un et Vn en fonction de Xn et Yn et en déduire leur expressions en fonction de n.
Xn + Yn = Un + Vn + Un - Vn
Xn + Yn = 2×Un
|
et |
Xn - Yn = Un + Vn - Un + Vn
Xn - Yn = 2×Vn
|
| Donc on a : |
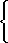 |
Un = |
Xn + Yn
2 |
= |
3×5n - 1
2 |
| Vn = |
Xn - Yn
2 |
= |
3×5n + 1
2 |
|
|
Exercice 2 : Soit la suite W définie pour tout n ∈ ℕ par : Wn = 3n - 2n + 1.
1. Calculer W0, W1, W2 et W3.
W0 = 30 - 2×0 + 1 = 2 ; W1 = 31 - 2×1 + 1 = 2 ;
W2 = 32 - 2×2 + 1 = 6 ; W3 = 33 - 2×3 + 1 = 22 ;
2. On pose Sn = W0 + W1 + ... + Wn. Calculer S3.
S3 = W0 + W1 + W2 + W3 = 2 + 2 + 6 + 22 = 32.
3. Montrer que W peut s'écrire comme la somme d'une suite arithmétique U et d'une suite géométrique V. Préciser leur raisons et leur premiers termes.
Les formes explicites des termes principaux d'une suite arithmétique et d'une suite géométrique sont respectivement : Un = r×n + U0 et Vn = V0×qn.
On a donc Wn = Un + Vn avec Un = -2n + 1 et Vn = 3n.
U est une suite arithmétique de premier terme U0 = 1 et de raison r = -2
V une suite géométrique de premier terme V0 = 1 et de raison q = 3.
4. On pose Un = U0 + U1 + ... + Un et Vn = V0 + V1 + ... + Vn.
a. Donner les expressions de Un et Vn en fonction de n.
On utilise les expressions des sommes des premiers termes d'une suite arithmétique et d'une suite géométrique.
| D'où Un = |
(n + 1)× |
(U0 + Un)
2 |
= (n + 1)× |
(1 - 2n + 1)
2 |
= |
(n + 1)(2 - 2n)
2 |
= 1 - n2 |
| et Vn = |
V0 - Vn+1
1 - q |
= |
1 - 3n+1
1 - 3 |
= |
-1 + 3n+1
2 |
b. En déduire l'expression de Sn en fonction de n. Vérifier la valeur de S3 et calculer S9.
Wn = Un + Vn donc Sn = Un + Vn.
| Soit Sn = 1 - n2 + |
-1 + 3n+1
2 |
= |
2 - 2n2 - 1 + 3n+1
2 |
= |
1 - 2n2 + 3n+1
2 |
| D'où S3 = |
1 -2×32 +34
2 |
= |
1 -18 +81
2 |
= 32 et |
S9 = |
1 -2×92 +310
2 |
= |
1 -162 +59049
2 |
= 29444 |
|