Retour | Index | Suite

Problème d'application.

Recherche d'un volume maximal

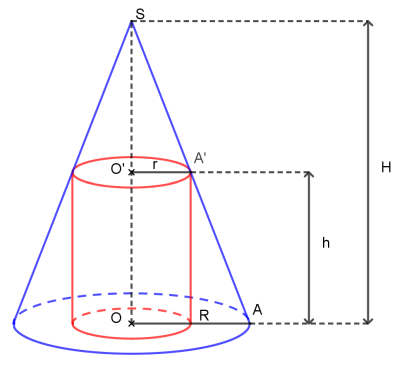
Problème 1 : Cylindre inscrit dans un cône.
Soit une cône de sommet S et de hauteur OS = H dont la base est un disque de rayon OA = R.
Un plan parallèle à la base coupe la hauteur du cône en O'. La section obtenue est un disque de rayon O'A' = r.
On pose OO' = h et on note V(h) le volume du cylindre de hauteur h et de rayon r.
1. Montrer que r = R× (H - h)
H
2. En déduire que V(h) =  Π R2
H2		 ×h(H - h)2
3. Calculer la dérivée V'(h) et étudier les variations de V(h) sur [0 ; H].
4. Pour quelle valeur de h le volume est-il maximum ?

1. Le plan étant parallèle à la base du cylindre, les droites (OA) et (O'A') sont parallèles. De plus, les droites (OO') et (AA') sont sécantes en S.
D'après le théorème de Thalès on peut écrire :  OA
OS		  =  OA'
O'S
Or les points O, O' et S sont alignés donc O'S = OS - OO' = H - h.
Par conséquent on a :  R
H		  =    r  
H - h		  d'où r = R× (H - h)
H
2. Le volume d'un cylindre de rayon r et de hateur h est Πr2×h, donc
V(h) = Π(R× (H - h)
H		 )2×h  soit V(h) = Π R2× (H - h)2
H2		 ×h =  Π R2
H2		 ×h(H - h)2

3. R, H et Π sont des constantes. On pose f(h) =  Π R2
H2		 ×h et g(h) = (H - h)2
On a alors f'(h) =  Π R2
H2		  et g'(h) = -2(H - h)
Par suite V(h) = f(h)×g(h) et V'(h) = f'(h)×g(h) + f(h)×g'(h)
Soit V'(h) =  Π R2
H2		 ×(H - h)2 - 2×h× Π R2
H2		 ×(H - h) =  Π R2
H2		 ×(H - h)(H - 3h)
V'(h) = 0 ⇔ h = H ou h = H/3 et V'(h) < 0 pour h ∈ ]H/3 ; H[
  0   H/3   H
signe de V'(h)   +  0 -  0
variation
de V(h)		     V(H/3)    
  ↗   ↘  
4. D'après le tableau des variations de V(h) le volume du cône est maximal pour h = H/3.
V(H/3) =  Π.R2
H2		 × H
3		 × (H -  H
3		 )2 =  Π.R2
H2		 × H
3		 × ( 2H
3		 )2 =  4Π.R2H
27

Remarque: Le problème peut être traité avec comme variable le rayon r.
On obtient V(r) =  Π.H
R		 (R - r)×r2  qui admet un maximum sur [0 ; R] pour r = 2R/3

Problème 1' : On peut chercher le volume minimal du cône dans lequel est inscrit le cylindre.
Les inconnues sont alors R et H. Les caractéritiques du cylindre, r et h étant données.
Les dimensions du cône doivent donc être plus grandes que celles du cylindre : H > h et R > r.
On étudie les variations du volume du cône, c'est-à-dire  1
3		 πR2H en remplaçant R ou H,
sur les intervalles ]h , +∞[ ou ]r , +∞[

Eléments de réponse : La relation r×H = R×(H - h) est toujours valable.
On en déduit : R =   r×H 
H - h		   ou H =   R×h 
R - r
On obtient V(H)=  1
3		 πr2   H3  
(H - h)2		    ou   V(R)=  1
3		 πh   R3  
R - r		  ; r et h sont des constantes.
On etudie alors le signe de V'(H) ou de V'(R)...