Définition et propriétés

Il n'existe qu'une et une seule fonction définie et dérivable sur ℝ telle que sa dérivée est elle même et dont l'image de 0 est 1. Cette fonction est la fonction exponentielle notée exp(x).
On a donc exp'(x) = exp(x) et exp(0) = 1

Les propriétés de cette fonction sont les similaires à celles des puissances.

exp(x+y) = exp(x)×exp(y)

exp(-x) = 1/exp(x)

exp(x-y) = exp(x)/exp(y)

(exp(x))n = exp(n x)

Lien avec les suites

On utilise plus souvent l'écriture e^x avec le réel e = exp(1) ≃ 2,718
En effet, pour x = 1, l'égualité (exp(x))ⁿ = exp(n x) peut s'écrire exp(n×1) = (exp(1))ⁿ = eⁿ
Cette expression est valable pour n entier relatif, mais est généralisable pour tout reél.

Cette notation, eⁿ peut être considéré comme le terme général d'une suite géométrique (U_n). Son premier terme est 1 est sa raison q = e.
En effet, si on pose U_n+1 = e×U_n et U₀ = 1, on a :
U₁ =e×U₀ = e ; U₂ =e×U₁ = e×e = e² ; ...; U_n = eⁿ
De la même manière, pour tout réel a, (exp(a))ⁿ = exp(an) soit encore e^an = (e^a)ⁿ, terme général d'une suite géométrique de premier termer 1 et de raison e^a.

Avec cette notation, les propriétés précédentes s'écrivent alors :

ex+y = ex×ey

e-x = 1/ex

ex-y = ex/ey

(ex)n = en x

Signe et variations

La fonction exponentielle est strictement positive et strictement croissante sur ℝ.

Par conséquent, on a :

a > b ⇔ ea > eb

et

a = b ⇔ ea = eb

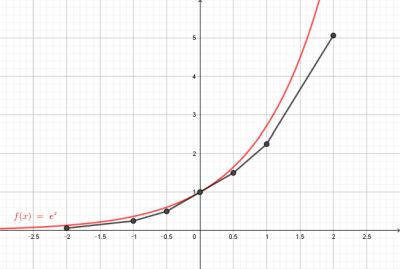
Courbe représentative

On suppose qu'il existe une fonction f dérivable sur ℝ telle que f' = f et f(0) = 1.
En s'appuyant sur le fait qu'au voisinage d'un point, une courbe et sa tangente en ce point sont très proches, on peut construire une « approximation » de la courbe représentative de cette fonction.

En partant du point de coordonnées (0 ; 1) avec des pas de 0,5 ou -0,5 on arrive à la courbe approchée en noir. La courbe rouge étant celle de la fonction exponentielle "exacte".