Index | Suite

Produit scalaire dans le plan

Définition

  • Si on considère deux vecteurs non nuls→u et→v, le produit scalaire de→u par→v est le nombre réel noté→u.v→(on dit→u scalaire v→) défini par
    →u.v→=→∥u∥ × ∥v∥→× cos(u→;→v) où→∥u∥ et ∥v∥→sont les normes des vecteurs→u et→v c'est-à-dire leur longueurs.
    Dans le cas où→v =→u, on a→u.u→=→∥u∥2.
    On note ce nombre→u2 et on l'appelle carré scalaire de→u.

    Remarque : Si l'angle géométrique entre les vecteurs est de 90° (angle orienté ±π/2), le cosinus est nul.
    Par conséquent, la condition pour que deux vecteurs soient orthogonaux est :→u.v→= 0.

    Autres définitions

  • Si on considère trois points distincts A, B et C tels que→AB =→u et→AC =→v on aura :
    →AB.AC→= AB × AC × cos(AB→;→AC) soit encore →AB.AC→= AB × AC × cos(BAC)^

  • Si le point H désigne le projeté orthogonal du point C sur la droite (AB), on obtient l'expression :
    →AB.AC→=-AB × AH-où-AB et AH-sont les mesures algébriques.
    Si les vecteurs→AB et→AH sont dans le même sens alors :

    →AB.AC→= AB × AH  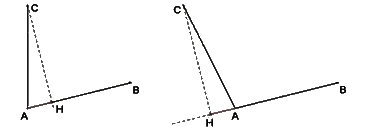  		 Si les vecteurs→AB et→AH sont de sens opposés alors :

    →AB.AC→= - AB × AH
  • Dans un repère orthonormal (orthonormé), si on considère→u(
    		•  x
    y    		 ) et→v( x'
    y'    		 ) alors 
    le produit scalaire s'écrit :→u.v→= x × x' + y × y'

    Propriétés

    Soient→u,→v et→w trois vecteurs non nuls. Soient k un réel non nul.
    →u.v→=→v.u→ Le produit scalaire est symétrique
    →u.( kv→) = k ×→u.v→ Le produit scalaire est linéaire
    →u.(v→+→w) = →u.v→+→u.w→  
    ( ku→). v→ = = k ×→u.v→ On dit également bilinéaire car
    (u→+→v). w→= →u.w→+→v.w→ "linéaire à droite" et "linéaire à gauche"

    • Autres expressions

  • Si on considère deux vecteurs non nuls→u et→v alors on peut écrire les égalités remarquables suivantes :
    (u→+→v)2 = →u2 + 2→u.v→+→v2
    (u→-→v)2 = →u2 - 2→u.v→+→v2
    (u→+→v).(u→-→v) = →u2 -→v2

  • Ainsi on en déduit les expressions du produit scalaire :
    • →u.v→=  1
    2    		 (∥u→+→v∥2 -→∥u∥2 -→∥v∥2)   et →u.v→=  1
    2    		 (→∥u∥2 +→∥v∥2 - ∥u→-→v∥2)
    Si on considère trois points distincts A, B et C tel que→AB =→u et→AC =→v
    alors la seconde expression devient :
    →AB.AC→=  1
    2    		 (AB2 + AC2 - CB2)  =  1
    2    		 (AB2 + AC2 - BC2)  (u→-→v = AB→-→AC = AB→+→CA =→CB)
    Si on a→AB =→u et→CA = →v, alors la première expression devient :
    →AB.CA→=  1
    2    		 (CB2 - AB2 - CA2)  =  1
    2    		 (BC2 - AB2 - AC2)  (u→+→v = AB→+→CA =→CB)

  • En ajoutant membre à membre les deux expressions de→u.v→on obtient :
    • 2→u.v→=  1
    2    		 (∥u→+→v∥2 - ∥u→-→v∥2)   Soit →u.v→=  1
    4    		 (∥u→+→v∥2 - ∥u→-→v∥2)
  • En retranchant membre à membre les deux expressions on arrive à :
    • ∥u→+→v∥2 + ∥u→-→v∥2 = 2→∥u∥2 + 2→∥v∥2
  • Dans un parallèlogramme ABCD on peut ainsi montrer que :
    →AB.BC→=  1
    4    		 (AC2 - BD2)    et    AC2 + BD2 = 2AB2 + 2BC2 (= AB2 + BC2 + CD2 + AD2)
    →AB.AD→=  1
    2    		 (AB2 + AD2 - DB2)  =  1
    2    		 (AC2 - AB2 - AD2)  (car AD→=→BC)
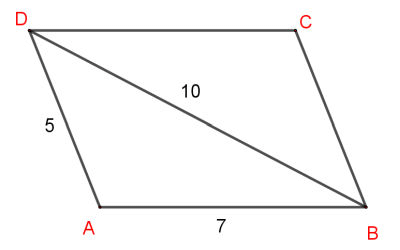
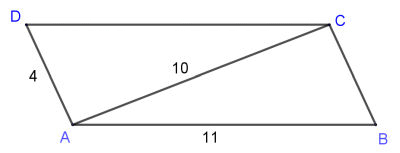
    →AB.AD→=  1
    2    		  (AB2 + AD2 - DB2)  →AB.AD→=  1
    2    		  (AC2 - AB2 - AD2)
    =  1
    2    		  (72 + 52 - 102) = -13  =  1
    2    		  (102 - 112 - 42) = -18,5