Calcul d'angles et de longueurs

formule d'Al Kashi

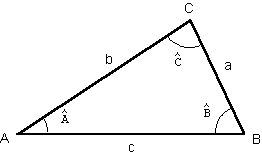
On considère un triangle ABC non aplati. On pose BC = a, AC = b et AB = c et on note ^A l'angle BAC^,^B l'angle ABC^et^C l'angle ACB^.
On reprend les expressions vues précédemment : →AB.AC→= AB × AC × cos(BAC)^et →AB.AC→=  1 2 (AB2 + AC2 - BC2)

En utilisant les notations de la figure, on peut écrire 2×c×b×cos(A)^= c² + b² - a²
Soit encore  a² = c² + b² - 2×c×b×cos(A)^ (formule d'Al Kashi).
Par rotation des variables on obtient : b² = a² + c² - 2×a×c×cos(B)^et c² = b² + a² - 2×b×a×cos(C)^

Remarque : Si l'angle est de 90°, on retrouve le théorème de Pythagore.

formule des sinus

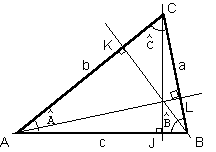
Dans un triangle ABC, les hauteurs issues des trois sommets peuvent s'exprimer de deux mannières. Pour la hauteur issue de C, en considérant les triangles ACJ et BCJ rectangles en J on a d'une part CJ = b × sin(A)^ et d'autre part CJ = a × sin(B)^. On a donc : b × sin(A)^= a × sin(B)^ que l'on peut écrire     b    sin(B)^  =     a    sin(A)^ Pour la hauteur issue de B, en considérant les triangles ABK et BCK rectangles en K on arrive à :

BK = c × sin(A)^= a × sin(C)^ que l'on peut écrire

c    sin(C)^

=

a    sin(A)^

En considérant les triangles ABL et ACL rectangles en L, la hauteur issue de A conduit à :

AL = c × sin(B)^= b × sin(C)^ soit

c    sin(C)^

=

b    sin(B)^

On peut donc résumer ces égalités par la relation :

a    sin(A)^  =     b    sin(B)^  =     c    sin(C)^

Théorème de la médiane
On considère un triangle AMB et le point I milieu du segment [AB]. La droite (MI) est donc la médiane issue de M. On cherche alors une expression "simple" du produit scalaire→MA.MB→.
En utilisant de la relation de Chasles on peut écrire :

→MA.MB→=	(MI→+→IA).(MI→+→IB)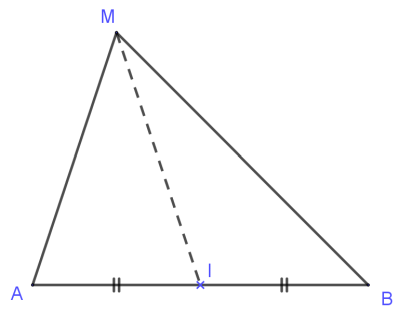
=	→MI.MI→+→MI.IB→+→IA.MI→+→IA.IB→
=	→MI2 +→MI.IB→+→MI.IA→+→IA.IB→ (car→u.v→=→v.u→)
=	MI2 +→MI.(IB→+→IA) +→IA.IB→
=	MI2 +→MI.0→+→IA.IB→ (car →IB + IA→= 0→)

=	MI2 + 0 -	→AB  2	.	AB→ 2	(car →IB = - IA→=	→AB  2	)

→MA.MB→=	MI2 -	AB2 4