Parabole

La courbe représentative d'une fonction du second degré est une parabole d'équation y = ax² + bx + c.
Cette courbe présente un sommet pour α = -b/2a. Ce sommet est un minimum si a > 0 ou un maximum si a < 0.
En effet, la dérivée de la fonction s'annule en changeant de signe pour x = -b/2a.

La droite x = α est un axe de symétrie. Cela signifie que si on s'écarte de part et autre de cette valeur α, les images des points obtenus sont identiques. En d'autres termes, si δ est un réel alors les points d'abscisses α - δ et α + δ ont la même ordonnée.
En effet, si la fonction du second degré est sous sa forme canonique a(x - α)² + β avec β = aα² + bα + c, on a : pour x = α - δ ; a(α - δ - α)² + β = a(-δ)² + β = a(δ)² + β
pour x = α + δ ; a(α + δ - α)² + β = a(δ)² + β

On peut également montrer qu'en faisant un changement de variable la fonction obtenue est paire. C'est-à-dire que pour tout X ∈ R, f(-X) = f(X). L'axe des ordonnées est alors l'axe de symétrie.
Si on pose X = x - α alors la fonction s'écrit f(X) = aX² + β et f(-X) = a(-X)² + β = aX² + β = f(X)

Remarques : Pour avoir sur un même graphe les deux fonctions il faut tracer f(x) et f(x + α).

Une fonction impaire est telle que f(-X) = -f(X). Elle présente un centre de symétrie (l'origine du repère).

Détermination de l'équation d'une parabole

On cherche à déterminer l'équation de la parabole d'après sa représentation graphique. Les paramètres à déterminer sont a, b et c. Il faut donc autant d'équations que d'inconnues.

* Si on peut repérer trois points A, B et C dont les coordonnées sont "facilement" lisibles, on pourra obtenir un système de trois équations à trois inconnues qui conduira à l'expression de la fonction du second degré.

Exemple : Déterminer l'expression de la fonction du second degré passant par les points A(-2 ; -3), B(0 ; -5) et C(1 ; 0).
Soit f(x) = ax² + bx + c cette fonction.
Si un point M(x_M ; y_M) est sur la courbe représentative de f alors y_M = f(x_M).
On traduit mathématiquement ceci pour les 3 points. On obtient le système suivant :

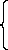	-3 = f(-2) -5 = f(0) 0 = f(1)	⇔		-3 = a×(-2)2 + b×(-2) + c -5 = a×(0)2 + b×(0) + c 0 = a×12 + b×1 + c
		⇔		-3 = 4a - 2b - 5 -5 = c 0 = a + b - 5
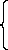		⇔		-3 = 4a - 2(-a +5) - 5 C = -5 b = -a + 5
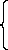		⇔		-3 = 6a - 10 - 5 C = -5 b = -a + 5
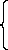		⇔		a = 12/6 = 2 C = -5 b = 3

La fonction recherchée est f(x) = 2x² + 3x - 5.

* Si le sommet S de la parabole peut être connu, il suffira d'un autre point pour pouvoir résoudre le problème.

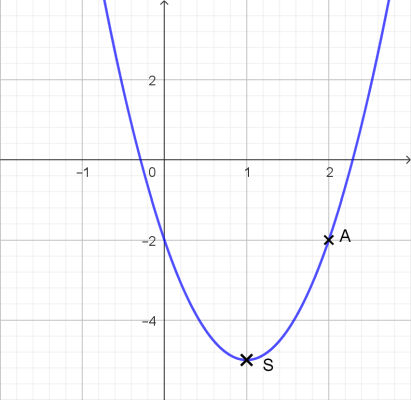
Exemple : Déterminer l'expression de la fonction du second degré de sommet S(1, -5) et passant par le point A(2 ; -2).
La forme canonique de cette fonction est f(x) = a(x - α)² + β avec α = -b/2a et β = f(α) = aα² + bα + c.
On est donc amené à résoudre le système suivant :

f(2) = -2 1 = -b/2a f(1) = -5

⇔

a×(2 - 1)2 -5 = -2 b = -2a a×12 + b×1 + c = -5

⇔

a = 3 b = -6 3 -6 + c = - 5

⇔

a = 3 b = -6 c = - 2

La fonction recherchée est : f(x) = 3x2 - 6x - 2 (fig. 1).

On peut aboutir au même résultat plus rapidement en condidérant f(x) = a(x -1)² - 5 car le sommet de la parabole est S(1 ; -5). On utilise le point A(2 ; -2) donnant f(2) = -2 pour trouver a. On développe pour en déduire b et c.

fig. 1		fig. 2

* Si les racines sont connues, il suffira également d'un seul autre point pour pouvoir déterminer l'expression de la fonction du second degré.

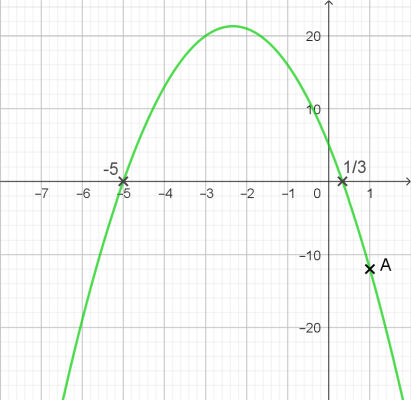
Exemple : Déterminer l'expression développée de la fonction du second degré admettant pour racines -5 et 1/3 et passant par le point A(1 ; -12).
La forme factorisée d'une fonction du second degré est f(x) = a(x - x₁)(x - x₂) avec x₁ et x₂ racines de l'équation f(x) = 0.
On peut donc écrire f(x) = a(x + 5)(x - 1/3).
De plus, on doit avoir f(1) = - 12 car la courbe passe par A(1 ; -12).
Ce qui conduit à : a(1 + 5)(1 - 1/3) = - 12 soit 6a×2/3 = -12 d'où a = - 3.
En développant, on obtient f(x) = -3(x + 5)(x - 1/3) = (x + 5)(-3x + 1) = -3x² - 14x + 5 (fig. 2).