Equation de cercle

Un cercle est caractérisé par son centre et son rayon. Un point appartient au cercle si sa distance au centre est égale au rayon.
Dans un repère orthonormé, le carré de la distance entre deux points A(x_A ; y_A) et B(x_B ; y_B) est :
AB² = (x_B - x_A)² + (y_B - y_A)². Pour ce calcul on peut utiliser les coordonnées du vecteur→AB.

Ainsi, si C désigne le cercle de centre O(x₀ ; y₀) et de rayon r alors un point M(x ; y) appartient à C si et seulement si : (x - x₀)² + (y - y₀)² = r²
Cette relation est une équation du cercle.

Si A et B sont deux points distincts, si le point M appartient au cercle de diamètre AB alors le triangle ABM est rectangle en M. Les droites (AM) et (BM) sont donc perpendiculaires et par conséquent les vecteurs →AM et BM→ sont orthogonaux.
Ainsi, on poura écrire : →AM.BM→= 0 ou →MA.MB→= 0.

Exemple : Soient les points A(-2;4) et B(4;0).
Déterminer une équation du cercle de diamètre [AB] en utilisant le produit scalaire de deux vecteurs. Puis en déduire les coordonnées de son centre et la valeur exacte de son rayon.

Soit M(x;y) un point du plan. On a alors→AM(

x + 2 y - 4

) et→BM(

x - 4 y

).

→AM.BM→= 0	⇔	(x + 2)×(x - 4) + (y - 4)×y = 0
	⇔	x2 - 4x + 2x - 8 + y2 - 4y = 0
	⇔	x2 - 2x + y2 - 4y - 8 = 0 (forme développée de l'équation du cercle)
	⇔	(x - 1)2 - 1 + (y - 2)2 - 4 - 8 = 0
	⇔	(x - 1)2 + (y - 2)2 = 13 (forme factorisée de l'équation du cercle)

Le cercle de diamètre [AB] a pour centre le point O(1;2) et pour rayon √13

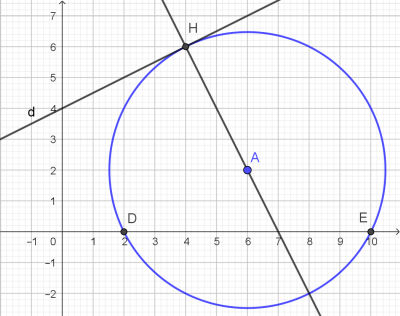
Exercice : Le plan est muni d'un repère orthonormé (O ;→i,→j).
On considère le point A(6 ; 2) et la droite d d'équation x - 2y + 8 = 0.
1. a. Donner les coordonnées d'un vecteur directeur à d.
Les coordonnées d'un vecteur directeur d'une droite d'équation ax + by + c = 0 sont→u(-b ; a).
Ici on aura →u(2 ; 1).

b. Déterminer une équation de la perpendiculaire à d passant par A.
Si M(x; y) appartient à cet perpendiculaire alors les vecteurs→AM(x -6 ; y -2) et→u(2 ; 1) sont orthogonaux et leurs produit scalaire est nul.
→AM.u→= 0 ⇔ (x - 6)×2 + (y - 2)×1 = 0 ⇔ 2x + y - 14 = 0.

2. Calculer les coordonnées de H, projeté orthogonal de A sur d.
H est le point d'intersection de la droite d et de sa perpendiculaire passant par A. Les coordonnées de H sont donc solution du système suivant :

{	x - 2y + 8 = 0	(a)	⇔	{	x - 2y + 8 + 4x + 2y - 28 = 0	(a)+2(b)	⇔	{	x = 20/5 = 4
	2x + y - 14 = 0	(b)			2x - 4y + 16 - 2x - y + 14 = 0	2(a)-(b)			y = 30/5 = 6

Les coordonnées de H sont (4 ; 6).

3. Déterminer une équation du cercle C de centre A passant par H.
Le rayon de ce cercle est la distance AH. Or les cordonnées du vecteur →AH sont (-2 ; 4)
et AH²= (-2)² + 4² = 20.
Par conséquent une équation du cercle considéré est : (x - 6)² + (y - 2)² = 20.

4. Le cercle C coupe l'axe des abscisses en D et E.
Calculer les coordonnées des points D et E.
L'équation de l'axe des abscisses est y = 0. On remplace y par 0 dans l'équation du cercle.
(x - 6)² + (0 - 2)² = 20 ⇔ (x - 6)² = 16 ⇔ x - 6 = 4 ou ⇔ x - 6 = -4 ⇔ x = 10 ou ⇔ x = 2 .
Les coordonnées des points sont D(2 ; 0) et E(10 ; 0).