Propriétes des angles orientés.

Angle géométrique

La mesure de l'angle géométrique formé par deux vecteurs est la valeur absolue de la mesure principale de l'angle considéré.

Relation de Chasles

Quels que soient les trois vecteurs non nuls→u,→v et→w on peut écrire :
(u→;→w) + (w→;→v) = (u→;→v).

Autres propriétés

Si on considère deux vecteurs→u et→v non nuls, alors on a (à 2kπ près) :
(v→;→u) = - (u→;→v)   ;   (-u→; -v→) = (u→;→v)   ;
(u→; -v→) = (-u→;→v) = (u→;→v) + π   ;   (u→;→u) = 0 et (u→; -u→) = π.
Si deux vecteurs→u et→v non nuls sont colinéaires alors :
(u→;→v) = 0 ou (u→;→v) = π.

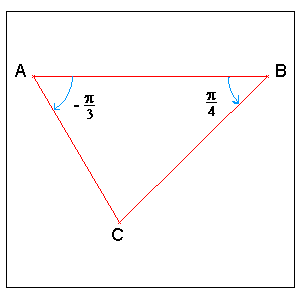
Exemple : Construire un triangle ABC tel que (AB→;→AC) = -π/3 et (BA→;→BC) = π/4. Calculer (CB→;→CA).

L'angle (AB→;→AC) est négatif on place donc les points A, B et C en tournant dans le sens des aiguilles d'une montre (sens indirect). (CB→;→CA) = (-BC→; -AC→) = (BC→; AC→) car (-u→; -v→) = (u→;→v).           = (BC→;→BA) + (BA→;→AC) D'après la relation de Chasles. Or (BC→;→BA) = - (BA→;→BC) car (v→;→u) = - (u→;→v). et (BA→;→AC) = (AB→;→AC) + π car (-u→;→v) = (u→;→v) + π. Donc (CB→;→CA) = -π/4 - π/3 + π = 5π/12

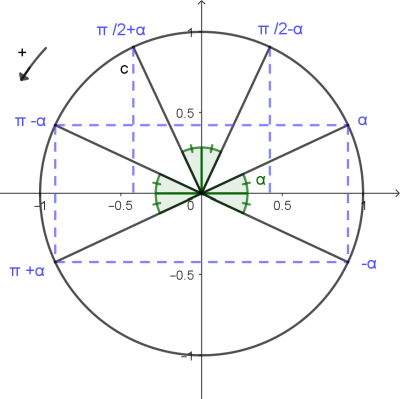
Formules de trigonométrie.

cos(- α) = cos(α)  ;  sin(- α) = -sin(α) cos( π 2  - α) = sin(α)  ;  sin( π 2  - α) = cos(α) cos( π 2  + α) = -sin(α)  ;  sin( π 2  + α) = cos(α) cos( π  - α) = -cos(α)  ;  sin( π  - α) = sin(α) cos( π  + α) = -cos(α)  ;  sin( π  + α) = -sin(α) cos(α + β) = cos(α)cos(β) - sin(α)sin(β) sin(α + β) = sin(α)cos(β) + cos(α)sin(β) cos(α - β) = cos(α)cos(β) + sin(α)sin(β) sin(α - β) = sin(α)cos(β) - cos(α)sin(β)

cos(2α) = cos2(α) - sin2(α) = 2cos2(α) - 1 = 1 - 2sin2(α)

sin(2α) = 2sin(α)cos(α) ; cos2(α) + sin2(α) = 1