Retour | Index

formules d'addition et de duplication des cosinus et sinus.

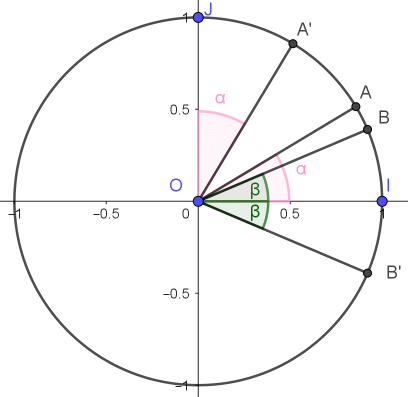
On considère le cercle trigonométrique dans le repère (O; I, J), comme indiqué sur la figure ci-contre.
On place les points A, B , A' et B' sur le cercle tels que :
(OI→;→OA) = α, (OI→;→OB) = β,
(OJ→;→OA') = -α et (OI→;→OB') = -β.
Ainsi, les coordonnées de ces points sont :
A(cos(α), sin(α))
B(cos(β), sin(β))
A'(cos(π/2 -α), sin(π/2 -α)) soit encore A'(sin(α), cos(α))
B'(cos(β), -sin(β))
On a alors :
→OA(cos(α), sin(α)),→OB(cos(β), sin(β))
→OA'(sin(α), cos(α)) et→OB'(cos(β), -sin(β))

  • Détermination de cos(α+β)
    On considère les points A et B'. (OB'→;→OA) = (OB'→;→OI) + (OI→;→OA) = α + β.
    Par conséquent :→OB'.OA→= OB' × OA × cos(α + β) = cos(α + β) car OB' = OA = 1
    Or on a également→OB'.OA→= cos(β)×cos(α) + (-sin(β))×sin(α)

    D'où le relation suivante : cos(α + β) = cos(α)cos(β) - sin(α)sin(β)

  • Détermination de cos(α-β)
    On considère les points A et B. (OB→;→OA) = (OB→;→OI) + (OI→;→OA) = α - β.
    Par conséquent :→OB.OA→= OB × OA × cos(α - β) = cos(α - β) car OA = OB = 1
    Or on a également→OB.OA→= cos(β)×cos(α) + sin(β)×sin(α)

    D'où le relation suivante : cos(α - β) = cos(α)cos(β) + sin(α)sin(β)

  • Détermination de sin(α+β)
    On considère les points A' et B. (OB→;→OA') = (OB→;→OI) + (OI→;→OJ) + (OJ→;→OA') = -β + π/2 -α
    D'où (OB→;→OA') = π/2 -(α + β).
    Par conséquent :→OB.OA'→= OB × OA' × cos(π/2 -(α + β)) = sin(α + β) car OB = OA' = 1
    Or on a également→OB.OA'→= cos(β)×sin(α) + sin(β)×os(α)

    D'où le relation suivante : sin(α + β) = sin(α)cos(β) + cos(α)sin(β)

  • Détermination de sin(α-β)
    On considère les points A' et B'. OA' = OB' = 1.
    (OB'→;→OA') = (OB'→;→OI) + (OI→;→OJ) + (OJ→;→OA') = β + π/2 -α= π/2 -(α - β).
    Ainsi →OB'.OA'→= OB' × OA' × cos(π/2 -(α - β)) = sin(α - β)
    Or on a également→OB'.OA'→= cos(β)×sin(α) + (-sin(β))×cos(α)

    D'où le relation suivante : sin(α - β) = sin(α)cos(β) - cos(α)sin(β)

  • Détermination de cos(2β)
    On considère les points B et B'. (OB'→;→OB) = (OB'→;→OI) + (OI→;→OB) = 2β.
    Par conséquent :→OB'.OB→= OB' × OB × cos(2β) = cos(2β) car OB' = OB = 1
    Or on a également→OB'.OB→= cos(β)×cos(β) + (-sin(β))×sin(β)

    D'où le relation suivante : cos(2β) = cos2(β) - sin2(β)

  • Détermination de sin(2α)
    On considère les points A et A'.
    (OA→;→OA') = (OA→;→OI) + (OI→;→OJ) + (OJ→;→OA') = -α + π/2 -α = π/2 -2α.
    Or cos(π/2 - x) = sin(x) et OA' = OA = 1
    Par conséquent :→OA.OA'→= sin(2α)
    Or on a également→OA.OA'→= cos(α)×sin(α) + sin(α)×cos(α) = 2cos(α)sin(α)

    D'où le relation suivante : sin(2α) = 2cos(α)sin(α)