Retour | Index | Suite

Résolution d'inéquations.

Inéquations du type cos(x) ≤ a ; cos(x) ≥ a ; cos(x) < a ou cos(x) > a.

  • Si a < -1 ou a > 1, il n'y a pas de solution car -1 ≤ cos(x) ≤ 1

  • Attention lorsque a = -1 ou a = 1...

    Exemple 1 : Résoudre dans ℝ les inéquations cos(x) ≥ 1 et cos(x) > -1.
    On sait que cos(x) ∈ [-1 ; 1 ] c'est à dire qu'on a -1 ≤ cos(x) ≤ 1.
    Les solutions de la première inéquation sont donc toutes les valeurs de x telles que
    cos(x) = 1, soit x = 2kπ, k ∈ ℤ.
    Pour la seconde inéquation, toutes les valeurs de R conviennent sauf celles pour lesquelles cos(x) = -1. Soit S = ℝ\{π + 2kπ,k ∈ ℤ}
    L'ensembles des solutions sur [-π ; π] serait S = ]-π ; π[
    et sur [0; ; 2π] on aurait S = [0 ; π[ ∪ ]π ; 2π]

  • Si a ∈ ] -1 ; 1 [
    On trace le cercle trigonométrique et la droite x = a.
    On surligne les parties du cercle dont les valeurs de x répondent à la question.
    On donne l'ensemble des solutions en tenant compte du dommaine de résolution...

    Exemple 2 : Résoudre sur [-π ; π] puis sur [0 ; 2 π] l'inéquation cos(x) ≥ 0,5.

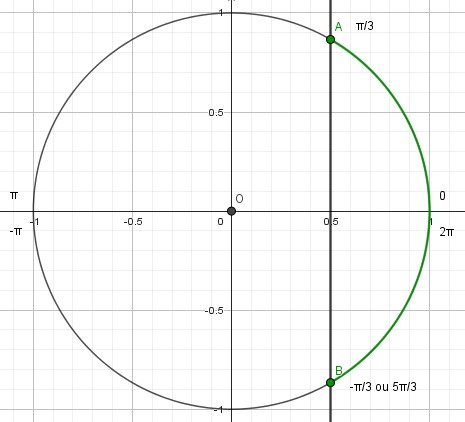
    Les points d'intersection de la droite x = 0,5 et du cercle sont A et B. Ils correspondent respectivement aux angles π/3 et -π/3 pour lesquels cos(x) = 0,5.
    L'ensemble des solutions sur l'intervalle
    [-π ; π] est donc S = [π/3 ; -π/3].

    Sur l'intervalle [0 ; 2π], on décrit le cercle dans le sans positif (sans inverse des aiguilles d'une montre) en partant de 0. On passe d'abord par le point A puis par le point B avant d'arriver à 2π. L'ensemble des solutions est alors :
    S = [0 ; π/3] ∪ [5π/3 ; 2π].

    • Inéquations du type sin(x) ≤ a ; sin(x) ≥ a ; sin(x) < a ou sin(x) > a.

  • Si a < -1 ou a > 1, il n'y a pas de solution car -1 ≤ sin(x) ≤ 1

  • Attention lorsque a = -1 ou a = 1...

  • Si a ∈ ] -1 ; 1 [
    On trace le cercle trigonométrique et la droite y = a.
    On surligne les parties du cercle dont les valeurs de x répondent à la question.
    On donne l'ensemble des solutions en tenant compte du dommaine de résolution...

    Exemple 2 : Résoudre sur [0 ; 2 π] puis sur [-π ; π] l'inéquation sin(x) < √3/2.

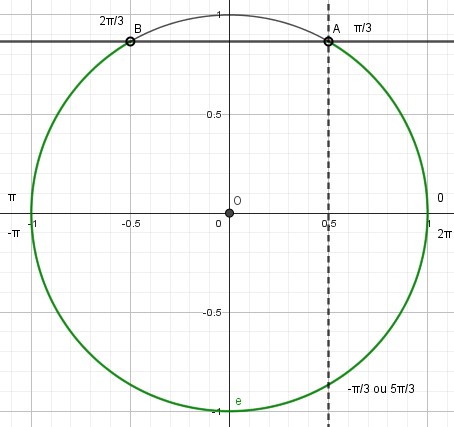
    Les points d'intersection du cercle et de la droite y = √3/2 sont A et B. Ils correspondent respectivement aux angles π/3 et 2π/3, pour lesquels sin(x) = √3/2. Ces valeurs seront à exclure de l'ensemble des solutions car l'inéquation est au sens "strict" (< au lieu de ≤). On surligne en vert la partie du cercle pour lequel le sinus des angles est inférieur à √3/2.

    Sur l'intervalle [0 ; 2π], on décrit le cercle dans le sans positif en partant de 0. La zone verte va ainsi de 0 à π/3 (point A) puis de 2π/3 ( point B) jusqu'à 2π. Les angles correspondants aux points A et B ne sont pas solution. On a donc :
    S = [0 ; π/3[ ∪ ]2π/3 ; 2π].

    Sur l'intervalle [-π ; π], on décrit le cercle dans le sans positif en partant de -π. La zone verte va de -π à π/3 (point A) puis de 2π/3 ( point B) jusqu'à π. L'ensemble des solutions est donc :
    S = [-π ; π/3[ ∪ ]2π/3 ; π].