Fonctions exponentielles

Fonction q^x avec q > 0.

Les fonctions exponentielles de base q sont un prologement sur R des suites géométiques.
Pour tout réel x, on les note: f(x)= q^x.

Propriétés

Si q > 1 alors la fonction : x↦q^x est croissante.
Si 0 < q < 1 alors la fonction : x↦q^x est décroissante.
Si q = 1 alors la fonction : x↦q^x est constante (pour tout x, 1^x=1)

Remarque : Le conportement en plus l'infini (+∞) est le même que pour les suites

Si q > 1 alors; lim
x→+∞ q^x = +∞ Si 0 < q < 1 alors; lim
x→+∞ q^x = 0

Autres propriétes

Les propriétés de q^x sont les mêmes que celles des puissances de 10 par exemple vues dans les classes inférieures.

q^x+y = q^x×q^y q^-x = 1/q^x q^x-y = q^x/q^y (q^x)ⁿ = q^n x

La fonction exponentielle

Parmi les fonctions exponentielles, une seule répond à la condition f'(0) = 1,
c'est la fonction exponetielle de base e notée parfois exp(x).

Le réel e ≃ 2,718, e > 1 donc la fonction exponentielle est strictement croissante sur R.
Pour tout x ∈ R, e^x > 0

Les propriétés précédentes sont toujours vérifiées :

e^x+y = e^x×e^y e^-x = 1/e^x e^x-y = e^x/e^y (e^x)ⁿ = e^n x

La fonction exponentielle étant strictement croissante sur R, on a :

a > b ⇔ e^a > e^b et a = b ⇔ e^a = e^b

La fonction exponentielle est dérivable sur R et a pour dérivée elle-même:
Pout tout réel x, exp'(x)= exp(x) = e^x

Pour tout x ∈ R, e^x > x
On pose f(x) = e^x - x. f est définie et dérivable sur R (somme de 2 fontions dérivables)

f'(x) = e^x - 1
La fonction f est donc
strictement croissante sur [0 ; +∞[
strictement décroissante sur ]-∞ , 0]
Elle admet un minimum pour x = 0
Or f(0) = 1 donc f(x) > 0, ∀ x ∈ R
e^x - x > 0 ⇔ e^x > x

f'(x) = 0 ⇔ e^x - 1 = 0 f'(x) > 0 ⇔ e^x - 1 > 0

⇔ e^x = 1 ⇔ e^x > 1

⇔ e^x = e⁰ ⇔ e^x > e⁰

⇔ x = 0 ⇔ x > 0

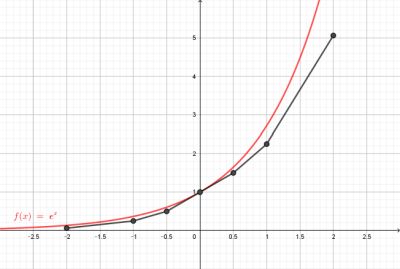
Courbe représentative

On suppose qu'il existe une fonction f dérivable sur R telle que f' = f et f(0) = 1.
En s'appuyant sur le fait qu'au voisinage d'un point, une courbe et sa tangente en ce point sont très proches, on peut construire une « approximation » de la courbe représentative de cette fonction.

En partant du point de coordonnées (0 ; 1) avec des pas de 0,5 ou -0,5 on arrive à la courbe approchée en noir. La courbe rouge étant celle de la fonction exponentielle "exacte".