|
Exemple 2 : (Antilles-Guyane septembre 2019 Exercice 1)
1. L'équation ln5 + ln(x + 1) = 1 a pour solution :
| a. x = e - 6 |
b. x = -1 |
|
d. x = -0,5 |
On doit résoudre cette équation sur l'intervalle I = ]-1 ; +∞[ (cf x + 1 > 0 soit x > -1)
| ln5 + ln(x + 1) = 1 ⇔ |
ln5×(x + 1) = ln(e) |
| ⇔ |
5×(x + 1) = e |
| ⇔ |
x + 1 = e/5 |
| ⇔ |
x = -1 + e/5 ≈ -0,45 > -1 (réponse c) |
2. Soit f la fonction définie et dérivable sur l'intervalle ]0 ; -∞[ par f(x) = 2ln(x) - x. Le nombre f'(2) est égal à :
| a. -1 |
b. 0 |
c. 2ln2 - 2 |
d. 2ln2 - 1 |
f'(x) = 2×(1/x) - 1 donc f'(2) = 2×(1/2) - 1 = 1 - 1 = 0 (réponse b)
3. Le plus petit entier naturel n solution de l'inéquation 2n > 175 est :
| a. n = ln(175/2) |
b. n = 7 |
c. n = 8 |
d. n = ln175 - ln2 |
| 2n > 175 ⇔ |
ln(2n) > ln(175) |
| ⇔ |
nln(2) > ln(175) |
| ⇔ |
n > ln(175)/ln(2) car 2 > 1 donc ln(2) > 0 |
Or ln(175)/ln(2) ≈ 7,45, le plus petit entier répondant à la question est 8 (réponse c)
|
|
Dérivée de la fonction logarithme népérien
La fonction ln est dérivable sur ]0 ; +∞[ et pour tout x > 0 ln'(x) = 1/x.
Dérivée de ln(u(x)) où u est une fonction dérivable strictement positive
Si la fonction u est dérivable et strictement positive sur un intervalle I alors la fonction ln(u)est dérivable sur I et :
(ln(u))' = u'/u
Exemple 3 : (Antilles-Guyane septembre 2018 Exercice 3)
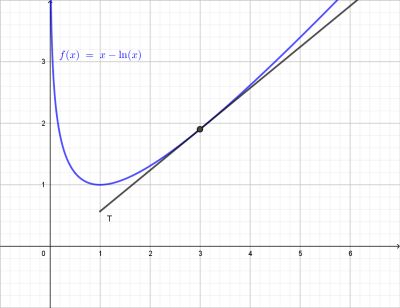
On considère la fonction f définie sur l'intervalle ]0 ; +∞[ par f(x) = x - ln(x).
On appelle Cf la courbe représentative de la fonction f dans un repère et T la tangente à
Cf au point d'abscisse x = 3.
Cette tangente T à Cf passe-t-elle par l'origine du repère ?
| Pour tout x > 0 on a : f'(x) = 1 - |
1
x |
d'où f'(3) = 1 - |
1
3 |
= |
2
3 |
et f(3) = 3 - ln(3). |
L'équation réduite de la tangente est de la forme y = f'(a)(x - a) + f(a) avec a = 3.
| Soit y = |
2
3 |
×(x - 3) + 3 - ln(3)= |
2
3 |
x - 2 + 3 - ln(3)= |
2
3 |
x + 1 - ln(3) |
L'ordonnée à l'origine n'est pas nulle donc la tangente ne passe pas par l'origine du repère.
(Prolonger la Tangente)
|
