Fonction convexe

Une fonction est dite convexe sur un intervalle donné, si sa courbe représentative est au-dessous de toutes les cordes.

Une fonction est convexe sur un intervalle si et seulement si :
- sa dérivée f ' est croissante sur cet intervalle.
- sa dérivée seconde est positive sur cet intervalle.
- sa courbe représentative est au-dessus des tangentes.

Exemple : La fonction carré est convexe. On a f(x)= x2 ; f '((x)= 2x et f "(x) = 2. - Pour tout réel x , on a bien f "(x) > 0 - La fonction 2x est bien une fonction croissante sur ℝ (fonction linéaire avec coéfficient directeur positif) - Les tangentes en un point d'abscisse a quelconque sont de la forme : y = 2a(x-a) + a2 = 2ax - a2. La fonction f(x) - (2ax - a2) = x2 - 2ax + a2 = (x - a)2 est une fonction du second degré. Elle s'annule pour x = a (point de contact), sinon elle est strictement positive. Ainsi, ∀ x ∈ ℝ ; f(x) - (2ax - a2) ≥ 0 soit f(x) ≥ 2ax - a2. La courbe est bien au-dessus des tangentes. Remarque : Soit deux réels a et b d'un intervalle I : Si f est une fonction convexe sur I alors : f( a + b 2 )  ≤   f(a) + f(b) 2

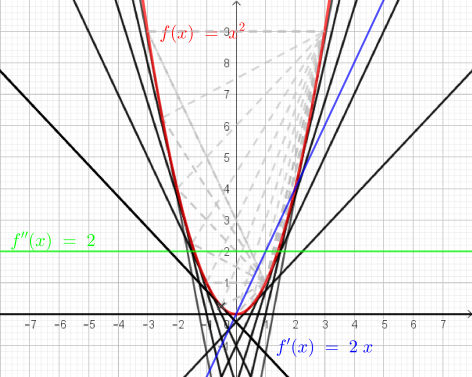
Noir : Tangentes : Pointillés Gris : Cordes

Pour le démontrer, on considère deux points de la courbe et leur milieu :
Soit A et B deux points d'une courbe représentative d'une fonction f et a et b les abscisses respectives.
On a donc A(a ; f(a)) et B(b ; f(b)). Les coordonnées du point I milieu du segment [AB]

sont : I(

a + b 2

;

f(a) + f(b) 2

)

Le point C situé sur la courbe ayant même abscisse que I à pour coordonnées :

C(

a + b 2

; f(

a + b 2

))

Etant donnée que f est une fonction convexe, les points du segment [AB] sont au-dessus de ceux situés sur la courbe.

Ainsi on a : yC ≤ yI soit encore f(

a + b 2

)  ≤

f(a) + f(b) 2

Fonction concave

Une fonction est dite concave sur un intervalle donné, si sa courbe représentative est au-dessus de toutes les cordes.

Une fonction est concave sur un intervalle si et seulement si :
- sa dérivée f ' est décroissante sur cet intervalle.
- sa dérivée seconde est négative sur cet intervalle.
- sa courbe représentative est en-dessous des tangentes.

Exemple : La fonction racine carrée est concave sur [0 ; +∞[. On a f(x)= √x dérivable sur ]0 ; +∞[ ; f '((x)= 1/2√x définie et dérivable sur ]0 ; +∞[ et f "(x) = -1/4x√x. - Pour tout réel x , on a bien f "(x) < 0 car x > 0 ; √x > 0 ; et -x < 0 ; - La fonction √x est croissante sur ℝ+* et l'intervalle image est ℝ+*. La fonction inverse 1/x est décroissante sur ℝ+*. Par conséquent la fonction composée 1/√x, est décroissante (cf. propriétié hors programme) - Démonstration dans le cas général : On étudie le signe de la fonction g(x) = f(x) - {f '(a)(x - a) +f(a)} ; on a alors g'(x) = f '(x) - f '(a). Ici f ' est décroissante. Si x ≥ a alors f '(x) ≤ f '(a) soit g'(x) ≤ 0. si x ≤ a alors f '(x) ≥ f '(a) et soit g'(x) ≥ 0. Par conséquent, la fonction g est croissant pour x ≤ a et décroissante pour x ≥ a. Elle admet un maximum pour x = a. Or g(a) = 0 donc g(x) ≤ 0. Soit encore f(x) ≤ f '(a)(x - a) +f(a). La courbe représentative est en-dessous des tangentes. Remarque : Soit deux réels a et b d'un intervalle I : Si f est une fonction concave sur I alors : f( a + b 2 )  ≥   f(a) + f(b) 2

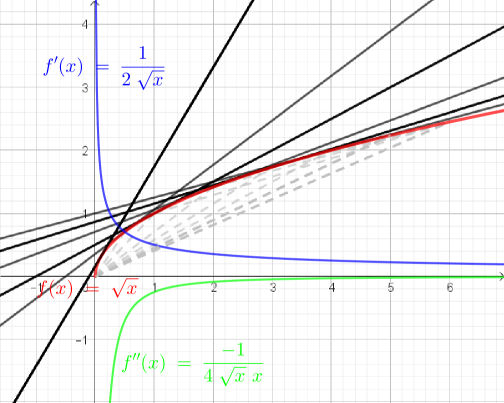
Noir : Tangentes : Pointillés Gris : Cordes

Point d'inflexion

On dit qu'un point est un point d'inflexion de la courbe représentative d'une fonction si la tangente en ce point traverse la courbe.

Au point d'inflexion la courbe change de convexité.
Un point est un point d'inflexion si et seulement si la dérivée seconde s'annule en changeant de signe.