Retour | Index | Suite

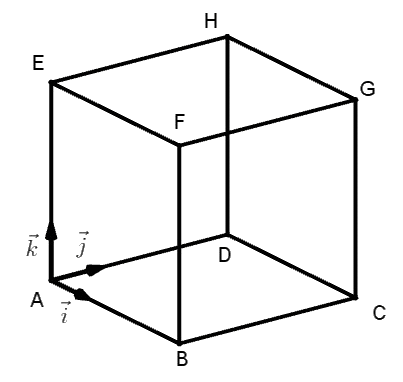
Exemple (D'après bac Asie 2022) : Le solide ABCDEFGH est un cube.
On se place dans le repère orthonormé (A ;→i,→j,→k) de l'espace
dans lequel les coordonnées des points B, D et E sont :
B(3 ; 0 ; 0), D(0 ; 3 ; 0) et E(0 ; 0 ; 3).

On considère les points P(0; 0; 1), Q(0; 2; 3) et R(1; 0; 3).
1. Placer les points P, Q et R sur la figure.(cliquer sur bouton 1.)

2. Montrer que le triangle PQR est isocèle en R.
On calcule les coordonnées des vecteurs→PR et→QR :
→PR(1 ; 0 ; 2)  et →QR(1 ; -2 ; 0)
On en déduit les distances PR et QR :
PR = √12 + 02 + 22 = √5 et QR = √12 + (-2)2 + 02 = √5
PR = QR donc le triangle PQR est bien isocèle en R.


3. Justifier que les points P, Q et R définissent un plan.
Les coordonnées des vecteurs →PR et→QR ne sont pas proportionneles donc ils ne sont pas colinéaires et forment ainsi un base du plan.

4. On s'intéresse à présent à la distance entre le point E et le plan (PQR).
a. Montrer que le vecteur→u(2 ; 1 ; -1) est normal au plan (PQR).
On calcule les produits scalaires suivants :
→u.PR→= 2×1 + 1×0 + (-1)×2 = 0 et →u.QR→= 2×1 + 1×(-2) + (-1)×0 = 0.
Le vecteur→u est orthogonal à deux vecteurs non colinéaires du plan (PQR), il est donc normal à ce plan.

b. En déduire une équation cartésienne du plan (PQR).
Méthode 1 : Le plan passe par P et un vecteur normal est→u. Tout point M(x ; y, z) du plan est tel que :
→PM.u→= 0 ⇔  (x - 0)×2 + (y - 0)×1 + (z - 1)×(-1) = 0
⇔  2x + y - 2z + 1 = 0 est une équation cartésienne du plan (PQR).
Méthode 2 : Une équation cartésienne d'un plan dont un vecteur normal est→u(2 ; 1 ; -1) est de la forme 2x + y - z + d = 0.
Le plan passe par P donc 2×0 + 1×0 -1×1 + d = 0 d'où d = 1. Une équation cartésienne du plan (PQR) est 2x + y - z + 1 = 0

c. Déterminer une représentation paramétrique de la droite (d) passant par le point E et orthogonale au plan (PQR).
La droite passe par E(0 ; 0; 3) et un vecteur directeur est→u(2 ; 1 ; -1) d'où la représentation paramétrique suivante :
x = 2t
y = t    avec t ∈ ℝ.
z = 3 - t

d. Montrer que le point L ( 2
3		  ;  1
3		  ;  8
3		 ) est le projeté orthogonal du point E sur le plan (PQR).
Le point L ∈ (d) et L ∈ (PQR), il existe donc un réel t tel que 2×(2t) + (t) - (3 - t) + 1 = 0 soit 5t -3 + t + 1 = 0
d'où t =  2
6		  =  1
3		 . Par conséquent les coordonnées du point L sont L(2× 1
3		  ;  1
3		  ; 3 -  1
3		 ) c'est-à-dire L( 2
3		  ;  1
3		  ;  8
3		 ).

e. Déterminer la distance entre le point E et le plan (PQR).
La distance entre E et le plan est la distance EL telle que :
EL2 = ( 2
3		 )2 + ( 1
3		 )2 +( 8
3		  - 3)2 = 4 + 1 + 1
9		  =  6
9		  D'où EL =  √6
3

5. En choisissant le triangle EQR comme base, montrer que le volume du tétraèdre EPQR est  2
3		 .
On rappelle que le volume V d'un tétraèdre est donné par la formule :
V =   1
3		  × aire d'une base × hauteur correspondante.
Si EQR est la base, la hauteur est EP = 2.
Le triangle EQR est rectangle E, son aire est   1
2		  × ER×EQ avec ER = 1 et EQ = 2. Soit 𝒜EQR = 1.
Le volume du tétraèdre est donc 𝒱 =  1
3		  ×1 × 2 =  2
3

6. Trouver, à l'aide des deux questions précédentes, l'aire du triangle PQR.
Si on considère le triangle PQR, le segment [EL] reprèsente la hauteur pour le tétraèdre EPQR.
Par conséquent, son volume 𝒱 =  1
3		  ×𝒜PQR× EL. On en déduit que 𝒜PQR =   3×𝒱
EL		  = 3×  2
3		  ×  3
√6		  =  6
√6		  =  √6