Fonction valeur absolue

La fonction valeur absolue est décroissante sur ]-∞ ; 0] et croissante sur [0 ; +∞[

Démonstration : Soient a et b deux réels tels que a < b ; (a - b < 0 ou b - a > 0).

Si a et b sont positifs alors |a| = a et |b| = b donc |a| - |b| = a - b.
Comme a - b < 0 la fonction est croissante sur [0 ; +∞[
Si a et b sont négatifs alors |a| = -a et |b| = -b donc |a| - |b| = -a + b = b - a.
Or b - a > 0 donc la fonction est décroissante sur ]-∞ ; 0]

Expression d'une fonction sans barres de valeur absolue

On considère la fonction f définie par f(x) = |3x + 2| - |1 - x|
On cherche le signe de chaque termes. On peut présenter cela dans un tableau.
On a : 3x + 2 = 0 pour x = -2/3 et 1 - x = 0 pour x = 1.


signe de
-∞
 
-2/3
 
1
 
+∞


3x + 2
 
-
0
+
¦
+
 


1 - x
 
+
¦
+
0
-
 



expression de
 
 
¦
 
¦
 
 



|3x + 2|
 
-3x - 2
0
3x + 2
5
3x + 2
 


|1 - x|
 
1 - x
5/3
1 - x
0
-1 + x
 




 |3x+2| - |1-x| 
 
-2x - 3
-5/3
4x +1
5
2x + 3
 


L'expression de la fonction est :
f(x) = -2x - 3 pour x ∈ ]-∞ ; -2/3]
f(x) = 4x + 1 pour x ∈ [-2/3 ; 1] 
f(x) = 2x + 3  pour [1 ; +∞[

Equations et Inéquations

Résoudre une équation du type | a | = | b | revient à résoudre a = b ou a = -b.

Résoudre une inéquation du type | a | < b équivaut à a < b ou -a < b
c'est à dire a < b ou a > -b soit encore -b < a < b.

Résoudre une inéquation du type | a | > b équivaut à a > b ou -a > b
c'est à dire a > b ou a < -b soit encore a < -b ou a > b

Remarque : | x - a | représente la distance entre a et x.
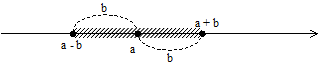
Résoudre | x -a | < b revient à chercher les valeurs de x telles que
-b < x - a < b c'est à dire telles que a-b < x < a+b

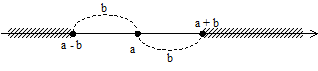
Résoudre | x -a | > b revient à chercher les valeurs de x telles que
x - a < -b ou x - a > b soit encore telles que x < a-b ou x > a+b

Exemple : Résoudre | x + 1 | > 5 et | 2x - 3 | ≤ 1
| x + 1 | > 5 équivaut à x + 1 > 5 ou x + 1 < -5 c'est à dire x > 4 ou x < -6
L'ensemble des solutions de la première inéquation est S = ]-∞ ; -6] &; [4 ; +∞[
| 2x - 3 | ≤ 1 équivaut à -1 ≤ 2x - 3 ≤ 1 soit 1 ≤ x ≤ 2
L'ensemble des solutions de la seconde inéquation est S = [1 ; 2]